Your students will use this collection of activity worksheets to learn how to solve for variables to simplify algebraic expressions. These sets of worksheets introduce your students to the concept of combining like terms, and provide examples, short practice sets, longer sets of questions, and quizzes. This is a paramount skill in algebra, you will need to master it in order to have an easy transition to higher level math. To combine like terms we either subtract or add numerical coefficients. You basically are cleaning up an expression or equation to just make it more workable. We suggest whenever you are evaluating expressions or equations to think about like terms first. This series of lessons and worksheets teach the steps for simplifying equations by matching or combining terms that are alike until there are no more steps that can be performed. A variety of equations are provided ranging from simple to advanced.
Print Combining Like Terms Worksheets
Click the buttons to print each worksheet and associated answer key.

Combining Like Terms (Difficult) Lesson
Follow along and simplify this expression: x2 + 3x2 + 6x2 + 8x2


Difficult Worksheet 2
Simplify for each. Students should have a good handle on the use of exponents for these problems. Example: 12x2 - 5 + 4x2 + 12.

Difficult Review Worksheet
Review the steps for simplifying an equation, then complete the practice problems. You will need to take this review. Example: x2+8x2+5x2+6x2

Combining Like Terms Difficult Quiz
This quiz will help you understand how to simplify expressions. For each problem, simplify. Then check your answers and record your total score below. Example: 15x2 - 10 + 3x2 + 15

Difficult Do Now
This worksheet is great to kickoff a class period. Complete the following problems, then put your answer in the "My Answer" box. Example: 8x2+50 - 4x2 - 2x = _____

Combining Like Terms Simple Lesson
These are more simple problems to work with. Follow along and simplify this type of expression: (-7 + 3y) - (2y - 3)

Simple Worksheet 1
For each, simplify the given equation. Some of these problems with get you going in the right direction. Example: 5n - 2(5-2n) + 2(4n-5) + 10 (4n - 2)

Simple Worksheet 2
Break these down into digestiable pieces for yourself. Start by putting things to together. Example: 14n - 2(2-3n) + 4(3n-1) + 2(4n-6)

Simple Combinations Review
Review the steps for simplifying an equation with one variable: (-4 + 2y) - (6y - 4)

Simple Like Terms Quiz
For each problem, simplify the given equation. Then check your answers and record your total score below. Example:

Simple Do Now
We label these as "simple", but they include many terms, so they may be a challenge for some students. Example: 7x + (x-5) + 3x - (2x-5) + 6x +2 =

Solving Equations (combine like terms) - Worksheet 1
Solve for each given equation by putting together all of the coefficients. Example: 10 + 6x + 2x = 18.



Worksheet 4
We are working to get everything to the other side of the equals sign. Example: 92 = 7x + 3x + 2



Solving Equations (combine like terms-with negatives) - Worksheet 1
Don't get tripped up by the operators here. Example: 3x + 9 - x = 15



(with negatives) - Worksheet 4
The negative values get a little harder to work with here. Example: 3 = -2x + x + 3

Combining Like Terms Lesson
Follow along with the steps below to solve this equation: (4x+7y) - 2(-3y + 2x). You will need to expand everything to get it going.


Practice the Skill
Simplify each equation as we show you in the first example. Example: 3(a+2) + 4(2a+5) + 8(4a-2)

Negatives Practice Worksheet
Simplify each equation shown. Example: 13m - 11m - 12m + 10m + 16 - 7 + 9m - 5m

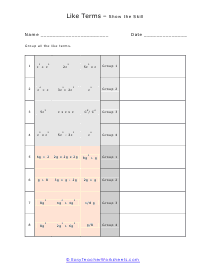
Show the Skill
See if you are ready to be a show off yet. Example: 20m - 12m - 14m + 8m + 11 - 6 + 3m - 2m


Meet the Skill 2
Do not let the exponents get in your way. An example problem here: -3x2 - 4x + 3 + x2 + 8x - 2





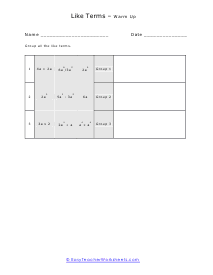
Warm Up 2
This one allows you a great deal of room to move around with. Example: -26x + 16 + x2 - 14x + 18

Complete the Equation Basic skills: Independent practice 1
These are perfect to get started with working on multiple terms that need to be packed together. Example: 12x + 5 + 5x + 4

Independent Practice 2
Solve each equation. You will work with basic terms and constants. Example: 12a + 15 - 9 - 3a

Intermediate Skills: Independent Practice 1
We introduce how to handle terms that have exponents. Example: 12x2 + 5y3 + 6x2 + 7y3

Like Terms Lesson
Learn how to group like terms in more complex expressions such as: a + a 3a - a 5a4 / a2

Like Terms - Try the Skill
For each problem simplify by grouping all terms in the given expressions. Example: y x y x y

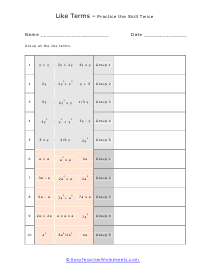
Like Terms - Practice the Skill
More practice sheets to move forward with this skill. Example: e + e 3e + 2e e2 x e2

Same Variable and Power Lesson
We walk you through the process of organizing these guys: a × a, a2, a3



Review Sheet
You are first reminded about the skill and then asked to work on your own. Then complete the practice problems. b × b x b2 x b3

Like Terms Quiz 2
For each problem, group the like terms, and then check your answers and record your total score below. Example: r × r x r2 x r3

How to Combine Like Terms in Math
Before we get into like and unlike terms in math, it is essential to look at algebraic expressions quickly. An algebraic expression is a mathematical expression that includes constants and variables and operators like addition and subtraction.
A variable is used for a term that’s value is not known, whereas the value of a constant term is definite. A variable usually comes with a numerical number known as a coefficient. Some examples of such algebraic expressions include 2x + 3x – 5, 5x – 10, 5x2 - 3xy + 8, etc.
Two like math terms have the same variables. This could be the base number or variable. It could also be a base variable that has the same exponent. As we advance with this skill, we will learn that coefficients can be different in like terms. For example, the value -4yz2 and yz2/3 are like terms. In order to solve equations and expression, you will combine like terms often. Often it the first step to solve just about anything in algebra. Be sure that you carry any math operator that is attached to the term. For example: 4y + 7x - 5y + 3x. The 5y carries the negative operator with it. When we combine this, we will end up with -1y + 10x. I like to urge students to underline like terms. If you have two like terms that involve the variable x and y, I would have them underline the x terms once. This would be followed by underlining the y terms twice.
Like Terms- What are They?
In an algebraic expression, terms are commonly differentiated by additional or subtraction. For example, there is only one term for a monomial expression. For instance, 5x, 3y, 6x, etc. Similarly, there are two terms in a binomial expression, such as 3y + x, 4x + 5, x + y, etc. There are three terms in a trinomial, while polynomials have several terms if they are of higher degrees.
In algebra, like terms are those that have identical variables and exponents, whatever their coefficients might be. In an algebraic expression, like terms are combined so that it is not difficult to calculate the result of the expression.
For instance, 6xy + 7y + 7xy is an algebraic equation. The terms of this equation are 6xy and 7xy. Hence, if you want to simplify this expression, you can combine the terms 6xy + 7xy + 7y = 13xy + y. it must be kept in mind that when you combine like terms in math, only the coefficients of the terms will be added.
Unlike terms, on the other hand, they do not have identical exponents and variables. For instance, an expression 9x + 4y contains terms because it has different variables that have not been raised to a similar power.
How to Combine Like Terms in Math
Now that you understand the theory, let’s learn how to combine like terms in math with some examples:
Example 1
Look at this expression: 3x + 4y
Since x and y have different variables, it is impossible to simplify this expression.
Example 2
If you want to simplify this expression 3x2 + 4x + 8y + 4x + 10x2, here is what you will have to do:
First, sort the terms so that your expression looks like this: 10x2 + 3x2 + 4x + 4x + 8y.
Then, solve the expression so that it comes to 13 x2 + 8x + 8y.
We can solve this expression because the terms have the same variables that have been raised to the same exponent as well.
Conclusion
When looking at like terms in math, all you need to keep in mind is that terms that have the same variables, as well as the same exponents are those that can be solved. With like terms, two things can be added or subtracted, depending on the kind of equation you are dealing with.
For example, you know that you can add the terms 3 + 4, and you will be left with a final answer, 7. The reason why you can solve this expression is that both the terms are numerical. Using the same logic, you cannot combine 2x + 3y because these are not like terms, meaning the expression will have to remain unsolved.


