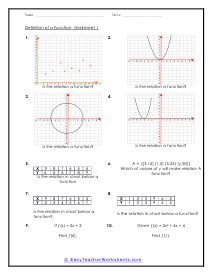
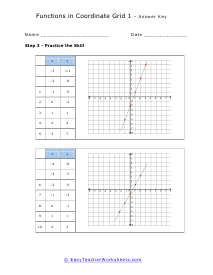
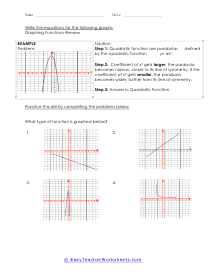
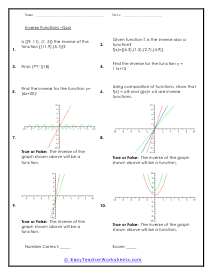
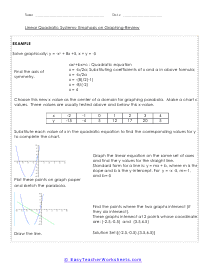
Functions are a relationship based system where you have a set of inputs and outputs that are the result of those inputs. Change your inputs and your outputs are affected as well. In math we use functions to model of form of relationship between two distant sets of elements. You can basically think of a function as a predetermined rule to how a variable fits in a set to direct an outcome. Functions can be stated in a wide range of ways including the use of tables, equations and words. A function is a solid means to model any mathematically environment we come across. Functions are at the root of polynomial equations, in that they represent the relationship between inputs (also called "arguments") and outputs, with the understanding that each single input must relate to only one output. Some functions are defined as a formula or algorithm, while others are represented by graphs or tables. However they are represented, every function describes how an input is to be manipulated within or by the function. For example, the function of squaring means that for every input x, the output will be x squared.

The following collection of activity sheets will introduce your students to mathematical functions. This series looks at all aspect of the use of functions. We will examine the cofunction of their use and how to write one. We will explore how to post an evolution to their nature and how to exponential change their overall outcome. The lessons will also introduce students to graphing functions and interpreting the nature of those graphs. We will also learn how to use a graph to predict future outcomes.