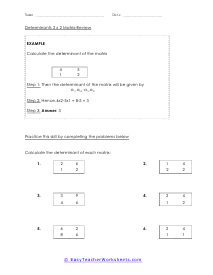
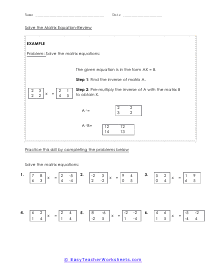
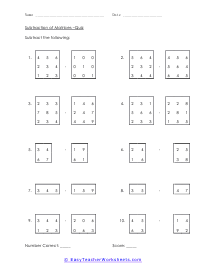
A matrix is a set of number or symbols that are arranged in rows and columns. Kind of like really small spreadsheets. A matrix can also contain expressions. Matrices often are a good option for working with multiple linear equations. We can often carry out operations between two matrices. Addition between two of them is pretty simple, as long as the matrices are the same size. You just need to add the values of matching positions. Subtraction follows the same pattern as addition. Multiplication is a bit more difficult and requires you to understand the dot product. We save that for that section of worksheets. The application of matrices math is a pivotal to rendering every single computer generated illusionary image you have ever seen, thus far. The math used helps determine the x, y, and even z position of the object and its movement. Basic matrix calculations also help electricians under the inner working of electric circuits. Matrix math has endless application in construction and textile design.
Matrices have been stumping students since the mid-19th century when it first discovered that they could be used to represent linear transformations. Even though a matrix is seen as a rectangular array they also come in several different forms. The most popular being rows, columns, squares, and diagonals. The worksheets in this section will help you learn how to apply basic operations to a matrix and series of them. They also demonstrate how to convert a matrix to other systems and how they relate within that system. Each section of matrix worksheets consists of a full step-by-step lesson, guided lessons, practice worksheets, and a quiz. We encourage you to walk through each progression at your own pace.