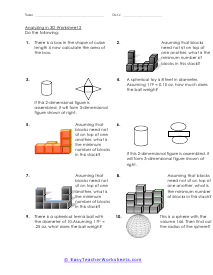
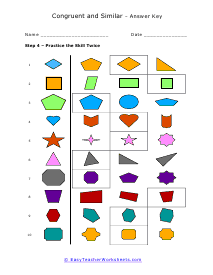
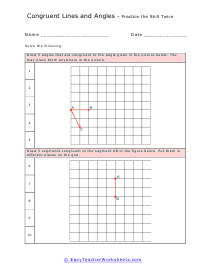
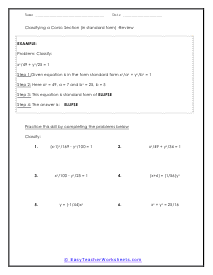
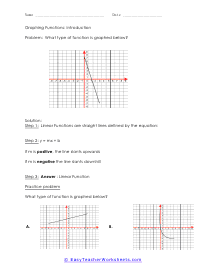
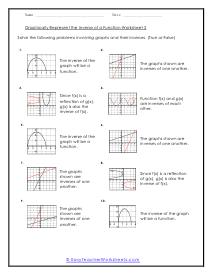
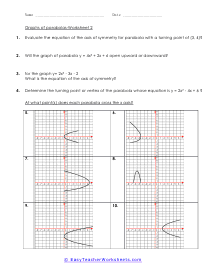
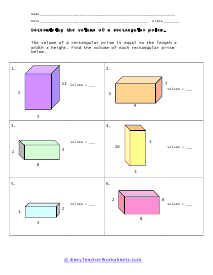
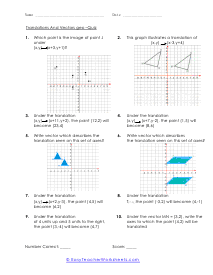
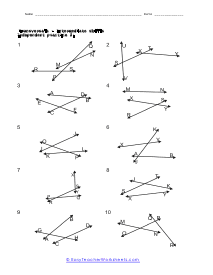
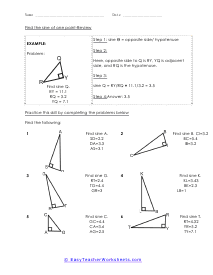
The branch of math that focus on the properties of shapes is called geometry. It is broken into two distinct disciplines plane and solid geometry. The plane form is all about studying flat objects and shapes. Whatever you could draw on a piece of paper. Solid geometry concentrates on three-dimension objects which is why it lends itself more to practical application whereas planar is more theoretical. Both can be very helpful; it just depends on the situation that you are encountering. We sometimes refer to geometry as the math for people that love Legos. This is because it is all about understanding shapes and measures within those shapes. There is two-dimensional geometry for flat shapes we call this plane geometry. In plane geometry you would explore simple shapes like circles, lines, and triangles; any shape you can draw on a standard piece of paper. When we start to look at three-dimensional shapes like cylinders and cubes we are working with solid geometry. Solid geometry has a ton of real world applications these are the applications that engineers spend their entire career working on.

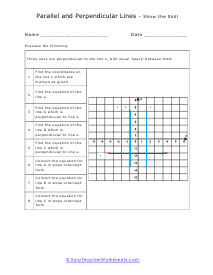
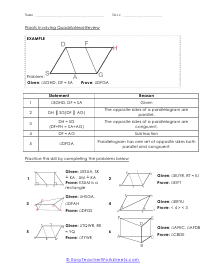
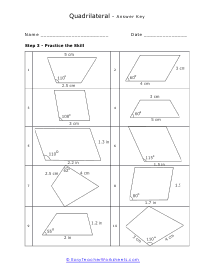
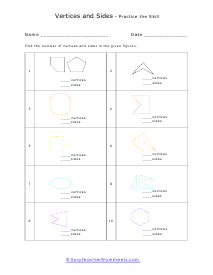
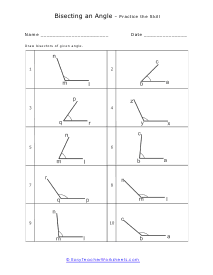
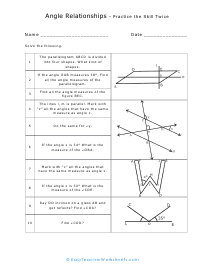
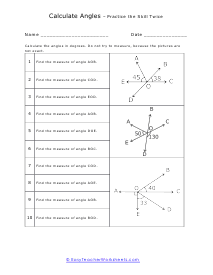
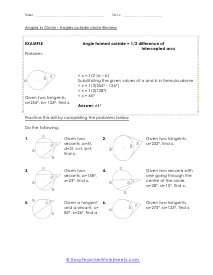
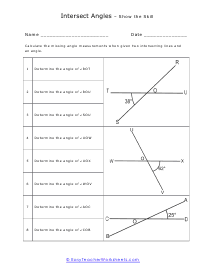
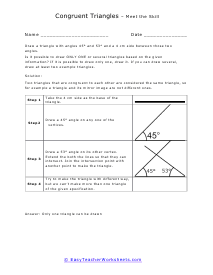
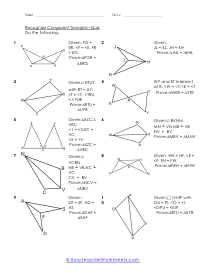
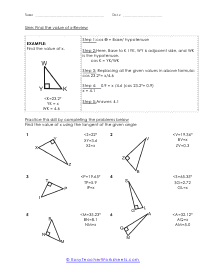
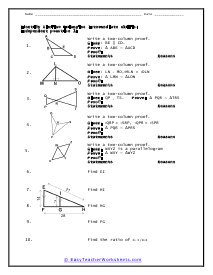
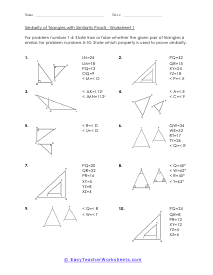
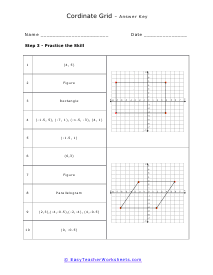
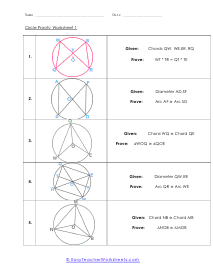
We start off with a pretty extensive section that is dedicated angle geometry. This is a very practical and highly sought after math skill. We continue on covering all of geometry 1 and 2 topics and skills this includes a great number of sheets on circle and triangle geometry. You should find that we have one of the largest collections of triangle worksheets. You will find an extensive catalog of worksheets available in this section please note that we have so many angle, circle, triangle geometry worksheets that we paired them together at the bottom of this page. Please be certain to scroll the entire way down this page. There are roughly a thousand geometry sheets available here. You will find handy answer keys available with everything that requires you to calculate just about anything.