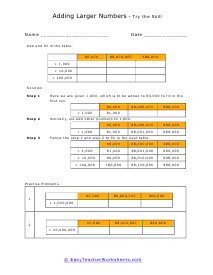
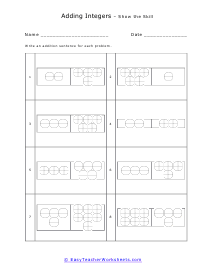
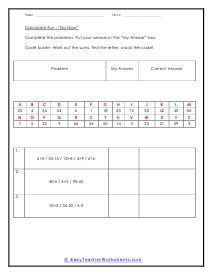
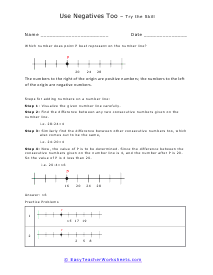
Integers are one of the five classification of real numbers that is often confused and not made clear to students. They include integers, irrational, natural, rational, and whole numbers. Whole numbers are positive values that lack a fractional or decimal value. Integers are show numbers that also include the other side of a number line, the negative values. Natural numbers are counting numbers, but do not include zero. Rational numbers are fractions of two integers (formed by a quotient). Irrational numbers are values that cannot be written as a fraction. Any number that is not a fraction or that does not have a fractional component to it is called an integer. Sometimes these are referred to as plain numbers as well. There are a few things that people often forget about integers because they stray from the simple definition itself. Since zero does not and basically cannot have a fractional component, zero is an integer. Also, all negative counting numbers are integers as well. Just because it has a negative symbol, does not mean it's not an integer.
The worksheets and lesson series that are available on this page feature a wide range of skills. Please note that everything is ordered by alphabetization. The reasons being that this is a topic that overlaps many different grade levels. We would encourage you to explore the different numbering systems available in this topic. We have over 350 integer worksheets for you below. Just click on the preview images below to find the worksheets that you are looking for.