This page will show you how to check if algebraic expressions are balanced through the use of the distributive property. Each set of worksheets introduces your students to the concept of the distributive property, and provides examples, short practice sets, longer sets of questions, and quizzes. You will often find this property used in many forms of math. It is simply a way to make calculating operations in a less complex fashion. They say there are so many ways to do problems, this is one of those methods that are different then most. These worksheets will help your students to learn how to use the distributive property to solve mathematical equations. They will also learn how to write equations their own equations using specific information provided.
Print Distributive Property Equations Worksheets
Click the buttons to print each worksheet and associated answer key.

Substituting Inside Equations Lesson
Learn how to use the distributive property to solve mathematical equations. Example: a x (b + c) = a x b + a x c.

Unique Spin
This puts a little mental math in there to show you a unique way to solve equations. You will also be given 2 practice problems to work on with it.

By the Variables
Solve these 10 problems by substituting the given values to the equation "a(b + c) = ab + ac." This worksheet can be used to ease students into using variables with equations.
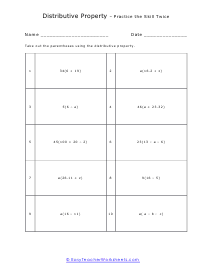
Live Problems Worksheet
Take out the parentheses and rearrange the equation. Students will work on manipulating the equations. Example: "45(100 + 20 - 2)"

Writing Expressions
Write these expressions using your understanding of the properties multiplication. Find their values in a, b, c. Example: 16 x 100 + 16 x 36

Warm Up: Two Expressions
For each of these three problems, write two expressions for the area accordingly (one for assuming the figure as on figure and second as a sum of two figures).

Substituting Solutions Lesson
Learn how to solve like 5(x + 14) = 22 - 3 using the properties of math. This lesson will walk through the process.

Equation Writing
Write an equation and solve based on the information provided: "When a number x is multiplied by 3 and 14 is subtracted from the result, the newly obtained result is multiplied by 4 this result equals to the sum of the same number x and 21."
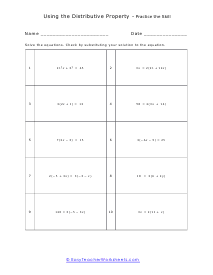
Intermediate Skill Worksheet
Solve the equations. This will be more advanced equations that require more steps to solve them. Check by substituting your solution to the equation. Example: 3x = 2(21 + 12x)

Deep Worksheet
Solve everything that is presented to you. Check by substituting your solution to the equation. Example: "A certain number x is equal to the sum of its opposite and 46."

The Solutions Show
You will work with more complex expressions and do you best to solve everything. Check by substituting your solution to the equation. Example: 2(5 + z) − 3z = 19 + 3

Warm Up
Write an equation and solve for these three statements. Example:
"Peter and Bill plow a field together. But peter did one and half times as much work as Bill. Find peter's earnings if they get $105 for total work? (Let Peter's salary be 'x')."
How to Use the Distributive Property with Algebra
The distributive property basically tells us that it does not matter how you package integers involved in multiplication. For example, if you had 3 bags of baseballs with 6 balls in each bag it would be the same number of baseballs, if you were to distribute all the balls in two bags. Parentheses often complicate algebraic expressions and equations. Students are often confused by how the number outside the parenthesis related to what is inside it. For example, when we are confronted with the problem 6 (3 + 4). We can solve it one of two ways. We could solve this by completing what resides inside in this format: 6 (7) which equals 42. We could also solve it by multiplying the outside and inside values such as: 6(3) + 6(4) = 18 + 24 = 42. The end result is the same thing. This gives you the option when performing these operations in algebra.
Mathematics was fun and easy to do before it involved letters and the variables that they represent into the mix. Since algebra became part of the curriculum, many students have faced difficulties solving problems. A major problem comes when adding algebra to the different properties of mathematics.
What Is It?
The distributive property explains that multiplying the totality of two or more addends with a number will have the same answer when each addended is multiplied separately by the number and then added together.
For addition we can represent it as: A x (B + C) = (A x B) + (A x C).
For subtraction it look more like this: A x (B - C) = (A x B) - (A x C)
A Simple Example
Let A = 3, B = 5, and C= 8. The equation then become: 3 x (5 + 8) = (3 x 5) + (3 x 8). Solving the left-hand side will give us 3 x 13 = 39. Solving the right-hand side will give us 15 + 25 = 39. Hence, Left hand side = right hand side.
The distributive property can make it easier to solve complex problems. It can be used to break down bigger numbers into the sum of two numbers before multiplying them. For example, if you were asked to multiply 7 x 28, it would be easier to use the distributive property of multiplication over addition to re-write the equation as 7 x (20 + 8), making it easier to solve.
In Algebra
In solving a simple question, such as 3 (4 + 6), we can either add the values in the parenthesis and then multiply them with 3, or we can multiply them separately and then add them up. However, algebra isn't always as easy.
In algebra, things are a bit more complicated than multiplying two numbers. In algebra, we work with unknown variables, giving us an expression of 3(x + 6). In this expression, we do not know what x is. One way of solving it would be to leave it as is, not simplify it, or we can use the distributive property.
We can simplify the expression using what we have learned into 3x + 18.
Let's see a bit more complex example. If you are given the equation 3(4x + 5y – 2z), you can use the distributive property to simplify that equation. In this case, you multiply 3 with the corresponding multiplicand, giving you (3 x 4x) + (3 x 5y) + (3 x 2z) =12x + 15y – 6z.
It can also work in the case of fractions. For example, if you are given the expression -½ (4y + 14), all you have to do is follow the distributive property to get you (-½ x 4y) + (-½ x 14) = -2y – 7.


