These worksheets will help you learn how to solve all different types of equations. We will start out very basic and move up to those that contain logs. This is a great selection of worksheets to compliment just about an level of algebra skills. As you start to work with these problems the best mindset to keep is working towards goals. Start by determining the variable you are attempting to find and step up all your steps from there. Algebra is very similar to puzzle solving. Equations often have similarities and that is why once you get the hang of this; it becomes very easy to do. These 3 series of lessons will help you teach your students how to: 1) Determine the value of a variable in a basic equation, and 2) Use logarithms to solve for an unknown variable.
Print Solving Equations Worksheets
Click the buttons to print each worksheet and associated answer key.

Moving Variables Lesson
Learn how to determine the value of a variable in an equation. Example: x + 1 = 9

Solve for X Worksheet 1
Solve for x for each of these 10 equations. These are two-step problems, mostly. For example these are the basic problem types: 7x + 4 = 494


Solving Equations Review
There is a short lesson at the top to show you how to solve equations with multiple instances of the the same variable. Follow the steps to solve for x: x + 4 = 12. The worksheet also contains 10 problems for you to finish.

Equation Quiz
Solve for x for each of these 10 problems, then check and score your answers below. Example: -64 = x - 76

Do Now Do Now
This is a great class activity to process together. They will have multiple instances of the same variables. So we get into combining like terms. Example: x+ 9 = 2x + 5

3 and 4 Step Lesson
Follow the steps to solve the following equation: x + 2 = 3x + (-16). This will help students become comfortable with 3 and 4 step equation solving.

3 Step Worksheet
You will work on solving the following types of equations: x + 9 = 18 + (-2x). You will work on 3 step problems.

Decimal Equation Worksheet
We get all decimally with these problems. Not all of them, but some have decimals in the equations. Here is an example: 6.2x - 5 = 7.9x + 3.5
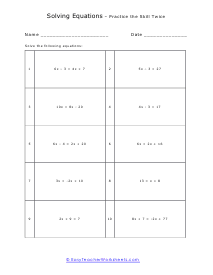
Lots of Steps Worksheet
You are going to have to take a few more steps than you are used to here. Example: 6x - 3 = 4x + 7 (2)
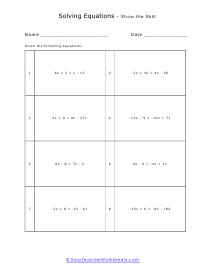
Many Moves Worksheet
Your primary goal should be to get your variables and constants together. Example: 2x + 9 = 9x - 271

Equation Warm Up
This will get you fluid with this skill and ready to tackle bigger problems. Example: -14x + 8 = -8x + 248

Basic Skills: Solving Equations Practice
For these 10 problems, solve for each variable. The problems are more 2 and 3 step problems. Example: 2x + 5 = 9

Basic Skills - Independent Practice 2
There are two instances of the variable in most of these problems. You will need to combine like terms. Example: 2x - x=8

Intermediate Skills Practice 1
The parentheses start to complicate things a bit here for you. Example: y - (2y+3) = 3(1 - 2y) - 6

Intermediate Skills Practice 2
These can be solved in just a few quick steps, but you will need to understand the process deeply. Example: 5x - (3x-1) = x-4

Intermediate Skills Practice 3
The last worksheet in the series. This is a bit challenging, but should be very doable for most students. Example: 2(a - 2) + 3(4a - 1) = 0

Solve for the Unknown Lesson
The next 4 worksheets are all for more advanced learners. Students will learn how to solve problems like the following: log2 b + log2 49 = 9. Then practice using the problems given below them.

Unknowns Worksheet 1
Logs rear up on this worksheet. Students should be comfortable with logs to handle these problems. Example: log6 289 + log6 a = 3.48

Solve for the Unknown Worksheet 2
For these 10 problems, solve for the unknown. These are slightly more advanced problems. Example: log2 16 + log(2) 144 = 5

Higher Level Review Worksheet
Not the easiest problems, but not that bad when you plan it out. The types of problems that you will see on here resemble this: log2 t + log2 144 = 289

Unknowns Quiz
Complete these 10 problems, then check and score your answers below. Example: log6 54 + log6 r = 3.12

Solve Them Do Now
Here is an e xample problem from this worksheet: log6 125 + log6 h = 3.01. These are slightly more complex equations to work with.
How to Solve an Algebraic Equation
You must be wondering; what place do letters have in mathematics? Well, letters have had quite a significant role to play in the world of mathematics since algebra was invented. The importance of mathematics is easy to note through the frustration you experience when solving word problems.
Johnny has trees that produce twice as many apples as he currently has. His friend gifts him three apples. Knowing that Johnny now has 17 apples, how many did he initially have?
Now try solving the following equation.
2x + 3 = 17
How easy was that? Imagine a world where people used language to explain an equation that could easily be translated through algebra! What a difficult world that would be.
Now that we have established the importance of numbers in math, let's figure out how to solve an algebraic equation.
What are Algebraic Equations?
Equations are statements in mathematics with two expressions on either side, separated by an equal sign. Algebraic equations contain letters as well as numbers. Letters stand for variables, whereas numbers are constants. Equations can include single and double variables, depending on complexity.
Solving equations is not hard if you look at them as a way to explain complicated situations using numbers. This viewpoint helps give you perspective and view mathematical equations as a challenge rather than an impossible feat.
The most important thing to remember about equations is that they are 'equal,' meaning that whatever you apply to one side to solve the equation needs to be applied to the other. Simplification allows for easy problem-solving. Once the equation is simplified, it is solved.
How to Solve an Algebraic Equation?
There are many different kinds of algebraic equations. However, they can be broadly categorized into two main kinds. We have single-variable and multiple-variable equations (further split into two or more variables).
1. Single Variable Equations
These are relatively easy to solve. The easier the equation, the lesser time it will take you to reach the solution.
The first kind is pretty simple, and the answer lies within the question.
x = 2
Here, the solution to the algebraic question is hidden in the question. The answer is "x=2."
However, consider the second example below.
2x – 1 = 11
What we need to prioritize here is to bring x to one side. However, we cannot simply take it there.
2x – 1 + 1 = 11
To eliminate 1, we can add 1 to the left side. However, this means we also need to add 1 to the right side.
2x – 1 + 1 = 11 + 1
We are left with the following solution.
2x = 12
To further simplify the expression on the left side, we need to eliminate the multiple of 2. We can do this by dividing the left side by 2.
2x / 2 = 12
However, this means we also need to divide the right side by 2.
2x / 2 = 12 / 2
Much better! Now, all we need to do is calculate the results.
x = 6
Plugging the six back into the equation leads to 11, confirming our solution! This trick is a great way to test any sum you have solved.
2. Double Variable Equations
These equations can only be solved using simultaneous equations and are slightly more complicated than the regular single-digit equation! In fact, they deserve a guide of their own!
Final Thoughts
How to solve an algebraic equation?
The answer depends on the kind of equation you are supposed to be solving. However, the rules remain the same.
Isolate the x, and remember to apply everything on both sides!
How to Keep Your Equation Solving Skills Sharp
An equation just tells us that two things are the equivalent of one another. What ever is to the right and left of the equals symbol is equal to the each other. The goal of solving equation is to find a solution that could replace the variable or multiple variables. If there is just a single variable, this is not that difficult. The process is just to get that variable by itself. For instances in the example: 3x - 4 = 2 we would follow two steps to complete this. As long as we do the same time to both sides of the equation, we can counterbalance any operations that are taking place. In this example we can achieve this by added 4 to both sides and this would leave us with: 3x = 6. Using the same principle, we would divide both sides by 2 and be left with x= 2. You will run into problems that have more than one solution. This can be frustrating, but they are doable. In some instances, you may need to guess values in those situations and that is okay until you get more experience with these types of problems. You put our energy into working through algebraic equations by applying basic principles. These sets range in difficulty from basic to intermediate, and may involve exponents, and some logarithms. We are mostly focused on solving for the final unknown variable for each equation. This is one of the key skills in algebra. If you are good at it, it will serve you well in College and even the real world on a daily basis.
Solving equations can be frustrating for students. You need sharp equation-solving skills when working on simple or complex algebraic problems. Many students face problems in evaluating correct answers while solving mathematical problems. Teachers often struggle to teach them the correct methods of solving problems.
If you want to improve your equation-solving skills, we have some tips that can help. The following ways can help you improve your analytical thinking and problem-solving abilities.
Tips to Enhance Equation Solving Skills
Understanding Functions
The most common problem that students face in solving equations is understanding functions. Mathematical equations typically involve multiple functions, including addition, subtraction, multiplication, and division. These functions may be simple to understand alone. However, solving them together in a single problem can be overwhelming.
If you want to sharpen your problem-solving skills, you may need to understand the correct order and method of solving each function in an equation.
Learn New Concepts
One of the essential tips to improve your problem-solving skills is to focus on learning new concepts. Students often stick to the curriculum. They do not spend time learning new mathematical concepts and functions. One of the best ways is to try solving challenging problems without seeking the teacher’s assistance.
If you get stuck, review the concepts and try solving the problem again. You can improve your equation-solving by identifying the problem in your equations.
Always Do Extra
Mathematical functions can be frustrating. You may exhaust yourself by solving a few equations. While this may be correct, covering extra problems can help you perform better. You not only learn to perfect your skills but also improve your speed. To find challenging equations, you can look up Google and search for as many equations as you like.
It is crucial to start with simpler problems. Once you grasp them, you can gradually proceed with complex equations. However, you may not want to try too many new concepts daily. They may be difficult to absorb.
Create Your Own Equations
Creating equations is one of the best ways to improve your equation-solving skills. Students typically rely on the word problems listed in the curriculum books. Although these problems can be sufficient to teach the concepts, altering them with different scenarios can perfect your skills. Changing the values in word problems can also be effective.
You can start with changing the values in an equation. If you successfully evaluate the answer, proceed with changing the conditions in a statement. You can solve the problem under the new conditions and evaluate your answer.
Find Relevance In Daily Life
What many students fail to realize in the earlier stages of their schooling is that mathematics finds its relevance in our daily lives. If you solve word problems, you may be able to understand how we can incorporate mathematics into our daily tasks. When you solve an equation, try to relate it to real-world examples.
By applying your everyday tasks to your problem-solving activities, you can learn to perform better.
Learn Number Tricks
Mathematics is full of surprises. Every number has a significant and unique role in problem-solving. You can find resourceful materials online to learn about the role of numbers in multiplication and division. Using number tricks can save you time and frustration while solving equations.
Most number tricks apply to dividing and multiplying bigger numbers. You do not have to spend too much time simplifying complex numbers.
Wrapping Up
Solving equations may seem a troublesome task. However, you can improve your skills by using the methods mentioned above. If you want to find more tips, you can search online and work on your equation-solving skills.


