The best way to start with these worksheets is to explore the anatomy of an equation with your students. Once they grasp all the moving parts, its time to practice solving various algebraic expressions. Activities include converting word problems into expressions, identifying whether a variable's given value is correct, solving for variables, and more. This is often a very important topic for students to deeply understand. These worksheets help you to teach your students to think critically about equations and expressions that have unknown variables. Students will learn how to test a given value as a solution to an equation and how to solve equations when no value is given.
Print Understanding Equations Worksheets
Click the buttons to print each worksheet and associated answer key.

Equations Meet Them Lesson
Use the equation given to answer the following question: Is the given number a solution (root) to it? Here is an example problem for you: 8x - 9 = 24 x = 4

Homework Worksheet
Follow the steps to create and solve an equation in order to answer the following statement: When you add 7 and a secret number, you get 12. you will also be given 2 problems to practice with.

Work Backwards Worksheet
For each of the following 10 problems, solve to answer this question: Is the given number a solution (root) of the equation? Example: 2x + 7 = 17 x = 5

Making Them Worksheet
Express each of the following statements as an equation, and then find a solution. Example: When you add 8 and a secret number, you get 24.

The Value of z Worksheet
For each value listed in the table, solve to answer this question: Which value of the variable z makes the equation true?

Classroom Worksheet
Solve these 3 equations as a class. They are very basic and should just serve as a reminder. Example problem: 2x = 750

True Equations
Follow the steps to answer this question: is the given value (x = 4) a solution? 13 = x/2 + 8. You will certify many different problems like that.

Fill in Expressions Worksheet
Follow the steps to fill in either the word "equation" or "expression". Then solve the problems by filling in the blanks. Find the value of _________ x/5 + 9, when x =5.

Is it Correct?
For each problem, is the given value a solution to the equations? Example: 10x = 8x - 20 when x = -10

Equation Solver
Solve these 10 problems by rearranging things to get the variables isolated. Example: 2x + 9 = 9x - 271


Warm Up
Based on the number given in each problem, answer the following question:
The equations PT = 5.3265p tells you to find the price with tax (PT) when the original price (p) is.
How to Check Solutions of Equations
The solution of an equation is the value or values of the variable(s) that make the equation true. In other words, it is a way of finding out what x is when you know what y is. Several methods can be used to check whether a given solution of an equation is correct.
Substitution
This is probably the most straightforward method. To use substitution, simply plug the given value of the variable into the equation and see if it makes the equation true. For example, let's check to see if x = 3 is a solution to the equation 2x + 5 = 11. Plugging in x = 3, we get,
2(3) + 5 = 11
6 + 5 = 11
11 = 11
Since the equation is true when x=3, we can conclude that x = 3 is a proper solution.
Graphical
Another way to check whether a given solution is correct is to graph both sides of the equation on a coordinate plane. The solution is correct if the two lines intersect at the given point. For example, let's check to see if x = 2 and y=1 is a solution to both of these y = 3x – 5 and x=2y. We can graph both sides of the equation as follows:
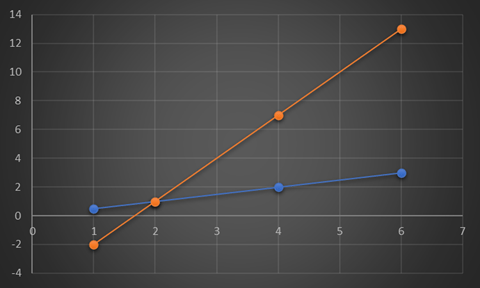
As we can see, the lines intersect at (2,1), which means that x = 2 is the correct solution.
Using Identities
Another way to check whether a given solution is correct is to use identities. Identities are equations that are always true for any value of the variable. For example, if you were given x2 - y2 = (x - y)(x + y) is an identity. If we plug in values for x and y, it will always be true. We can use this to our advantage to check whether a given solution is correct.
For example, let's check to see if x = 2 and y - 1 is a solution to y = 3x - 5 and x = 2y. We can rewrite it as follows:
y=3x-5
y=3(2)-5
y=1
and,
x=2y
2=2y
y=1
Now, we can use the identity x2 - y2 = (x - y)(x + y) to check whether x = 4 is a correct solution. We plug in x = 2 and y = 1 to get:
22- 12 = (2 - 1)(2 + 1)
4 - 1 = (2 - 1)(3)
3 = 3
Since the equation is true when we plug in x = 2 and y = 1, we can conclude that {2,1} is a correct solution.
Algebraic
Another way to check whether a given solution is correct is to use algebra. This method is probably the most difficult but also the most general. To use this method, you substitute the given value of the variable into the equation and see if you can simplify the equation to an identity.
For example, let's check to see if x = 2 is a solution to the equation 2x - 3 = 5. We can substitute x = 2 into the equation to get:
2(2) - 3 = 5
4 - 3 = 5
1 = 5
Since we could not simplify the equation to an identity, we can conclude that x = 2 is not a correct solution.
Wrapping Up
These are just a few methods that can be used to check whether a given solution is correct. There are many others as well. It is always a good idea to check your work, regardless of your m. This will help to ensure that you have found the correct solution.


