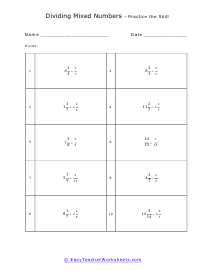
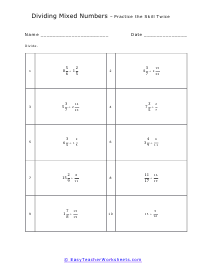
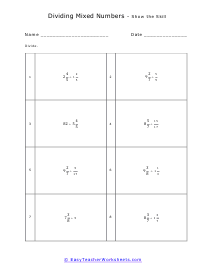
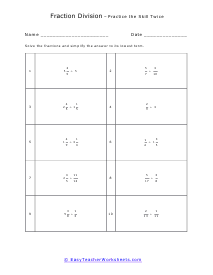
Students are often at a complete loss when they are asked to find the quotient of two mixed numbers. It is true that this math skill requires you to jump through a couple of hoops to pull off. The first step is always to convert the mixed numbers to improper fractions. This is easy when the denominators are the same, but if they are different you need to work that pony out first. Your next step is multiply the dividend by the reciprocal of the divisor. In most cases you will want to simplify whatever is left over.

How do you divide mixed numbers? A mixed number is a number that consists of a fraction and a whole number. For dividing mixed numbers, we first need to convert them into an improper fraction and then divide them like other fractions. Here we have enlisted a step-wise approach for dividing the mixed number. First, we need to multiply the denominator with the whole and add it with the numerator. For example, if we have 7 1/2 and 3 1/4 , you will multiply 7 x 2 + 1 = 15 and 3 x 4 +1 = 13. The obtained fraction will be 15/2 and 13/4. These two fractions are improper fractions that will be used for division. The sum we will get will be 15/2 ÷ 13/4. Next, we will take the reciprocal of the second fraction. So, the numerator will become the denominator, and the denominator will become the numerator. In this example, 13/4 will become 4/13. Also, when we take the reciprocal, the division sign will change into a multiplication sign. The sum will look like, 15/2 x 4/13. Multiply the numerators, 15 x 4 = 60 and the denominators 13 x 2 = 26. The fraction we will get will be: 60/26. Simplify the answer, if possible. In our example, the answer is divisible by 2. Simplifying the answer with 2, we will get, 30/13. Write the improper fraction in mixed form. Our answer will be, 2 4/13. These worksheets explain how to divide any combination of fractions, mixed numbers, and whole numbers.