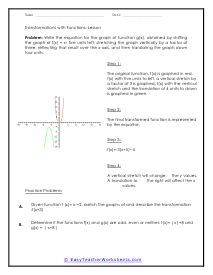
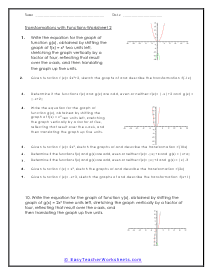
What are function transformations? One meaning of "to interpret" is "to change from one spot, state, structure, or appearance to another." At the angle when we take capacity and change its standard, so its diagram is moved to another spot on the hub framework, yet remains unmistakably a similar chart, we are supposed to be "deciphering" the function. For the most part, the transformation includes just moving the diagram around. Compressing or extending a grid is, even more, a "change" of the diagram. In any case, these two subjects are typically instructed simultaneously, and normally under a similar name. Know that the subject of "function transformation" frequently incorporates work change and the other way around. The last two simple changes include turning capacities over (flipping them around the x-axis), and reflecting them in the y-axis. The main, turning over, is found by taking the negative of the first capacity; that is, the standard for this change is - f (x). To perceive how this functions, investigate the diagram of h(x) = x2 + 2x - 3. When we move or re-position a graph of a function this is called a transformation. In this section you will be asked to graph a function and then transform it based on a fixed procedure. In most cases, you will be moving the graph up and down the y-axis or left and right of the x-axis. In many examples, we included a slight blue background to provide some contrast for you when you are printing this.
These worksheets explain how to transform functions to graphs and graphs to them as well. Your students will use these worksheets in order to practice transforming and graphing different functions. Students will also be asked to determine whether the transformed versions are equal, symmetrical, and more.