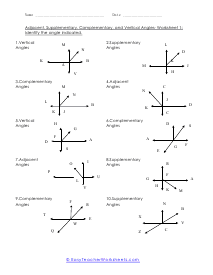
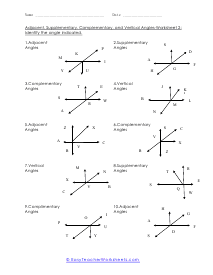
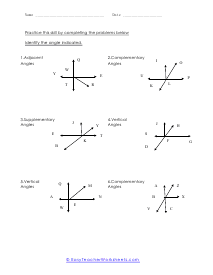
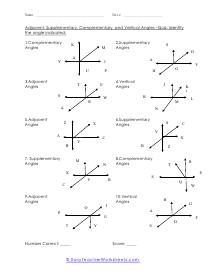
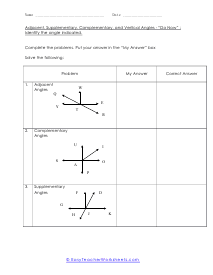
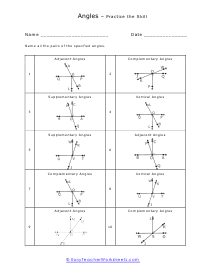
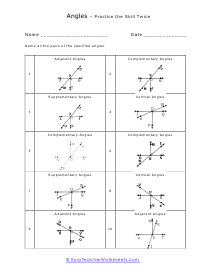
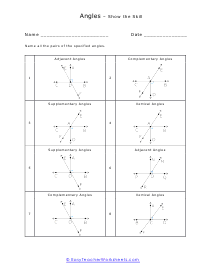
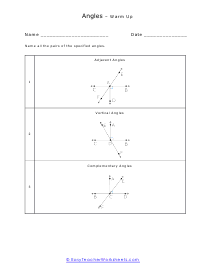
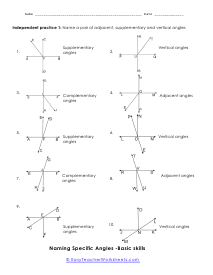
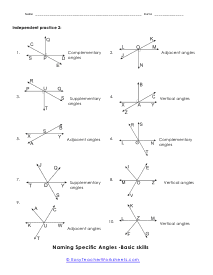
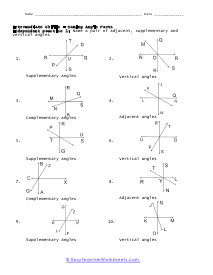
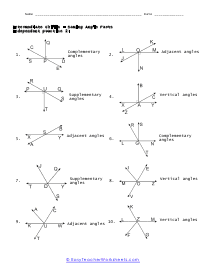
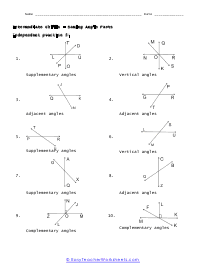
What are adjacent, complementary, supplementary, and vertical angles? Supplementary Angles - We define it with respect to the addition of two angles. When two angle's sum is 180 degree, and it forms a linear angle with each other, we will say such type of supplementary angles. If two angles form a linear angle like angle = 1 and angle (2) = 180 - x, the properties of angles will be same. Complementary Angles - If you are adding two angles of 90 degrees to form a right angle, you will call them complementary angles. In a condition of having one angle is x and the other one is 90 degree - x, we will use such complementary angles for trigonometric ratios. There will need a ratio complement another ratio by 90 degrees, for example; sin (90° - A) = cos A and cos (90° - A) = sin A, tan (90° - A) = cot A and cot (90° - A) = tan A. Here, trigonometric ratios of the angles are changing as they are complementing each other. Adjacent Angles - When two angles share the common vertex and side, it means it is an adjacent angle. Vertical Angle - If two lines are intersecting and four angles are forming, we will call those angles vertical angles or vertically opposite angles.

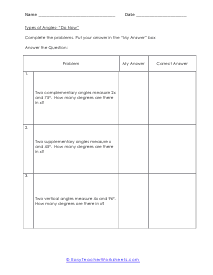
This collection of worksheets focuses your efforts on naming angles and finding measures with those angles based on your understanding of predefined angle relationships. The four angle relationships we focus on look at how two lines relate to each other. Adjacent angles are what I would refer to as angles that are touching because they share the same ray. Vertical angles are angles that are equal and directly across from each other. Supplementary angles are angles that when added equal 180 degrees. Complementary angle are usually part of a right angle and add up to 90 degrees. These worksheets explain how to adjacent, supplementary, complementary, and vertical angles and how to find the number of degrees in an angle(s).