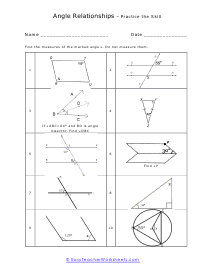
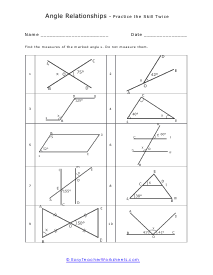
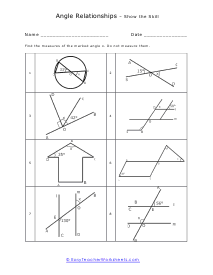
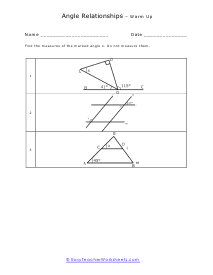
How do you identify relationships between angles? When two rays meet at a point, they form an angle at that point. These rays are also called the sides of a geometric shape. This is formed at the common endpoint, which is also called the vertex. There a wide variety of angle types and each of these has a unique set of properties. The different types of angles include congruent, adjacent, vertical, corresponding, exterior, and interior. You can measure these values by using a protractor and even use the properties of these measures and this is where relationships come into place. Comparing angles is also a common way to calculate the measure. These relationships include a comparison of the position, measurement, and congruence between two or more angles. Congruent angles no matter their orientation all have equal measures. Adjacent angles are when two lines cross each other; they form four angles. Any two angles are sharing a ray, line segment, or line. The angles that are not touching each other except at their vertex are vertical. Corresponding angles appear when a transversal crosses two other lines. Exterior angles are created with parallel lines and their transversal. Angles between the bounds of the two parallel lines are interior.
When you are given two parallel lines and a bisector you can tell a whole lot about the relationships between the angles. You will be given a set of parallel lines and a line that slashes through it. You then be asked to define the angles that ride off of those. You will need to understand the concept of supplementary and complementary angles to help you through these. You will also be presented with word problems that we force you to be reminded of triangle definitions such as isosceles and right triangles. These worksheets explain how to find the measurement of an angle by considering its relationship to what is known about the lines and angles in relationship with it. In many questions, students will not be allowed to measure directly.