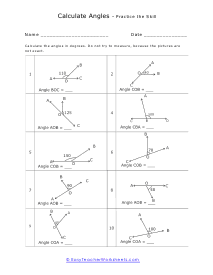
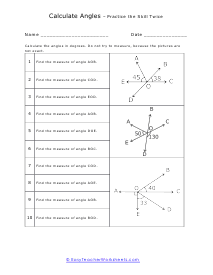
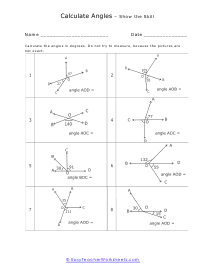
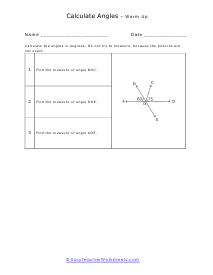
When we are confronted with angles that we are not sure the measure of we can use the environment around us to come up with a great deal of facts to determine those angles. How do you calculate the measures of angles using other known angles? In geometry, a point is a space between 2 beams (or line portions) with a similar endpoint (or vertex). The most widely recognized approach to gauge edges is in degrees, with a round trip estimating 360 degrees. You can ascertain the proportion of a point in a polygon on the off chance that you know the state of the polygon and the proportion of its different edges or, on account of a right triangle if you know the proportions of two of its sides. So as to figure the inside points of a polygon, you have to decide what number of sides the polygon has initially. Note that a polygon has an indistinguishable number of sides from it has points. The equation for finding the all-out proportion of every single inside point in a polygon is: (n - 2) x 180. For this situation, n is the number of sides the polygon has.

The worksheets in this section will give you unknown angles that you can find through the use of adjacent, complementary, supplementary and vertical angles. You are primarily always looking for the straight or right angle to work off of. Once you identify this angle, everything is downhill. These worksheets explain how to calculate the measurement of an angle. Your students will use these sheets to practice calculating angle degrees based on the relationship between other angles in the figure.