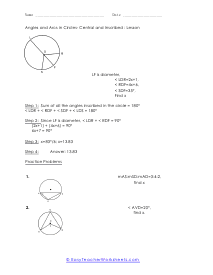
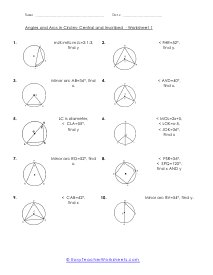
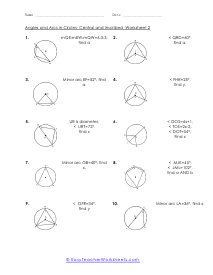
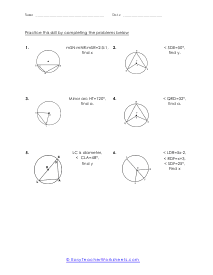
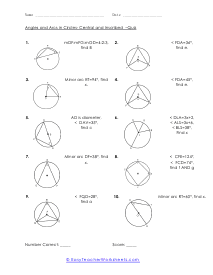
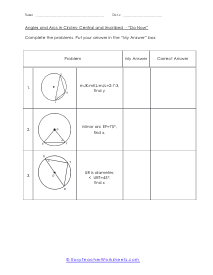
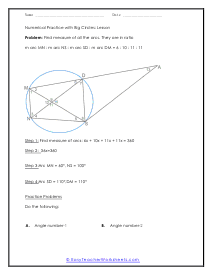
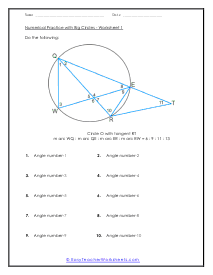
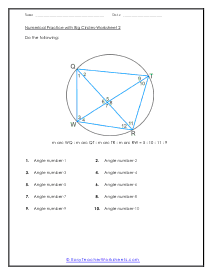
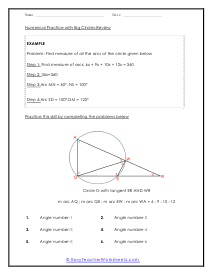
A portion of the circumference of a circle is the arch. You can measure an arch of a circle by finding the measure of the central angle or by finding the length of the arc itself. The sum all of all the inscribed angles in a circle are equal to one-hundred and eighty degrees. In many cases of this worksheet set you will be given a single measure and be asked to draw upon your knowledge of circle geometry to complete the unknown angles within it.

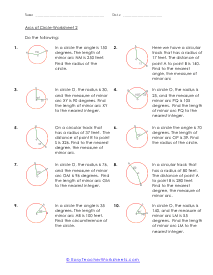
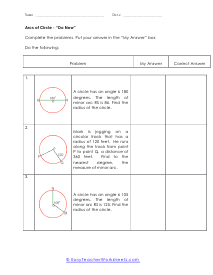
These worksheets explain how to find the length of an arc and the measure of an angle. Students will convert radians to degree and vice versa. Students will also learn about inscribed angles, and how to convert between units. What steps are needed to find the measures of arcs of circles? When studying to solve circles including their circumference and area, there is another measurement that you need to understand and that is arc length. It is a measure of the distance along the circumference of a circle. It represents a fraction of the circumference of the circle. So, how do you find the measures of arcs of circles? Before we get into the businesses, we need to understand that arcs can come from a central angle. The vertex of this is located at the center of the circle. You can measure an arc in two different ways: Angle: The measure of an arc as an angle is the same as the central angle that intercepts it. Length: The length of an arc is directly proportional to the circumference of the circle and is dependent on both the central angle and the radius of the circle. You can calculate the length of an arc is equal to the circumference times the fraction of the circle represented by the arc's measure. Length = (measure of arc/360) 2πr.