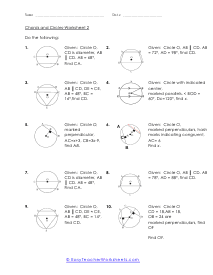
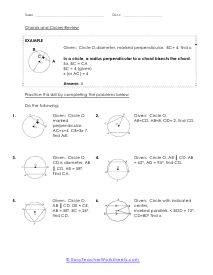
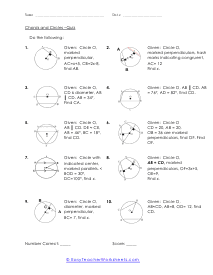
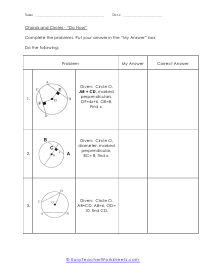
A chord of any circle is a straight line that starts and ends on the circle itself. In this section of worksheets we will be using the simple fact that a chord is a straight line to help us better understand all of the measures found engulfed by that circle. Please don't confuse chords with diameter. The diameter must pass directly through the center of the circle. Chords can chop through just about anywhere. You can say that chords do connect two point of a circle's circumference.

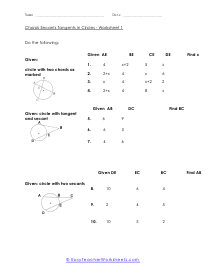
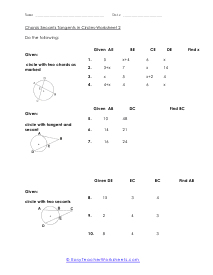
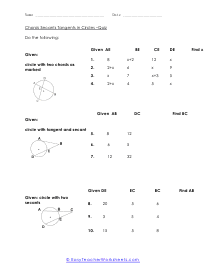
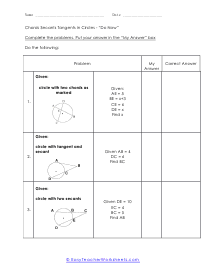
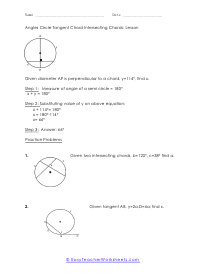
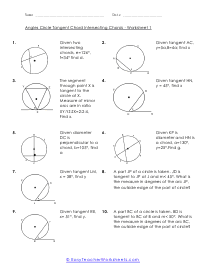
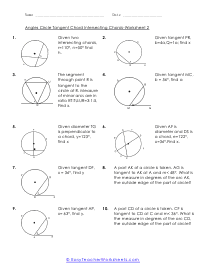
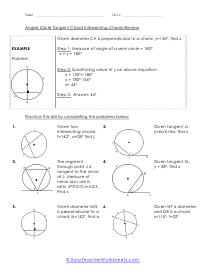
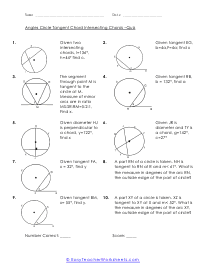
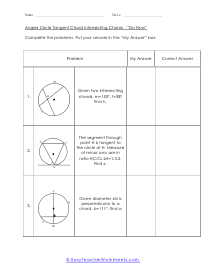
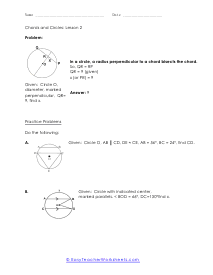
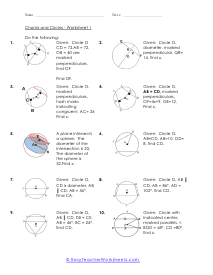
What are the chords that intersect circles? These are the two chords that you can intersect with each other in a circle, and the product of their segments are equal. If we draw a figure and name the two line segments A.B, it will be equal to segments C.D. Mathematically, AB = CD. Draw a circle. Mark two chords and intersect them into two segments at a particular point. The divided chords into two-line segments = A and B and, A × B = C × D. According to the theorem, no matter where you mark the chords, A multiply by B will always be equal to C multiply by D. These worksheets explain how find the measure of an angle between intersecting chords, as well as the value of chords. Your students will use the following sheets to learn how to solve for different variables (e.g. arc length, angles, line segments, and more) using the calculations for intersecting chords within circles.