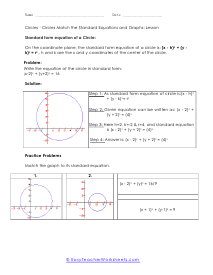
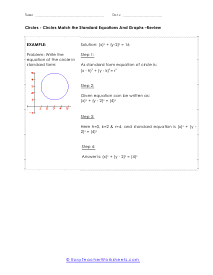
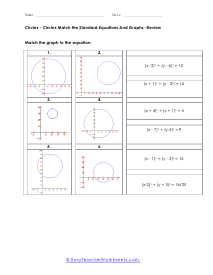
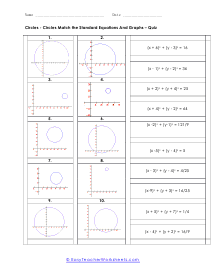
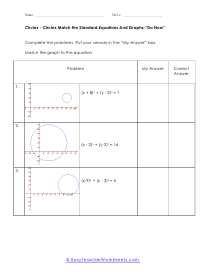
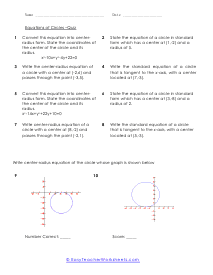
How do you find the equation of a circle? Every curve in a geometry is represented by an equation just like a straight line is represented by y=mx+b. There is an equation for a circle to, but how do we find it? The standard form of a circle is (x-h)2 + (y-k)2 = r2, this is when the center of the circle is not the origin. If this is the case we use the following equation; x2 + y2 = r2. Here, h and k are x-coordinate and y-coordinate of the center if the circle respectively, and r is the radius. When you know these numbers, you can easily find the equation of the circle.
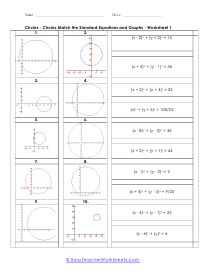
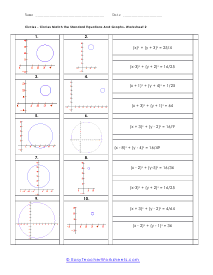
This batch of lessons and worksheets has us trying to make sense of the equations of circle on a coordinate grid. You will be asked to identify circle from their equation and also to create your own equation from a given circle. On the coordinate plane, the standard form equation of a circle is: (x - h)2 + (y -k)2 = r2 , h and k are the x and y coordinates of the center of the circle. In many cases you will be matching equations to circles. You will also need to determine the center and radius of the circles you are exploring.
These worksheets explain the standard form equation of a circle, and how to find the standard form, center, and radius of a circle. Students may also calculate circle circumference, diameter, etc.