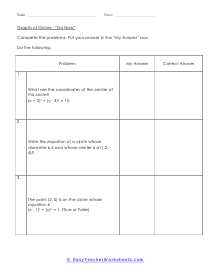
How to find the coordinates of the center of a circle? If you have 2 points on a circle, both X and Y figures are known, and a radius is given, you can find the center of the circle. Using the two given points as the center, draw two circles, each with the given radius. The point of intersection of these two circles are the possible points of center of the original circle. Algebraically, if the two points are (a,b) and (A,B), and the radius is r, you can solve these two equations (x - a)2 + (y - b)2 = r2 ::: (x - A)2+(y - B)2 =r 2 If there are three points provided, we can use them to find the center as well. Using these three points you can create three equations. (x1 - h)2 + (y1 - k)2 = r2 ::: (x2 - h)2 + (y2 - k)2 = r2 ::: (x3 - h)2+ (y3 - k)2= r2 You can then solve these equations and find the center of the circle.
When you are given an equation you can easily graph it on a coordinate grid by just plugging in any chosen values you see fit. In this section, you will prompted with a word problem or an equation and you will be asked to construct a circle based on this. It is often important to focus on the use of the y-axis. This determines the nature of most of what will be plotted on the graph. This is a fundamental skill that students will truly need to master before they start working with trigonometry.
These worksheets explain how to write the equation of a circle with a given center and radius. Your students will use the following sheets to learn how to write the equations of circles based on graph coordinates.