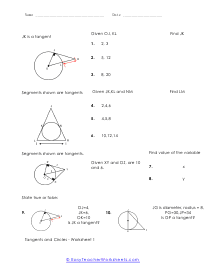
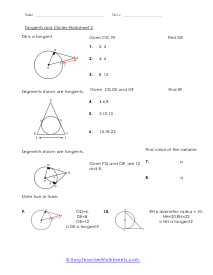
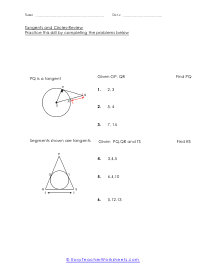
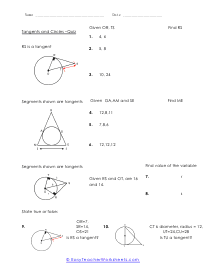
What is a tangent to a circle? It is a straight line that meets the circle at any point, and we will say this process the point of tangency. In this process, the tangent of the circle is perpendicular (⊥) to the radius. Here we have circle A where line segment AT is the radius, and congruent TP is the tangent to the circle. Hence, line segment AT is ⊥ to the radius TP Let's solve a question where line segment AT = 5 and radius TP = 12. How do we explore the length of the line segment AP? The angle T is a right angle. The reason is; the radius is perpendicular (⊥) to the tangent at the point of tangency. Hence, line segment AT is perpendicular ⊥ to radius TP. Here, it means we can use the Pythagorean Theorem to solve the questions for line segment AP. (AT)2 + (TP)2 = (AP)2 | 52 + 122 = (AP)2 | 25 + 144 = (AP)2 | 169 = (AP)2 | √169 = 13 = AP Any tangent to a circle is a straight line that passes through one point of the circle. The point that meets on the circle is called the tangency.
This can be very helpful for when we are looking to understand more about triangles that are occupied by the circle. This is a common mathematically technique that deck builders use to know how to properly anchor the footing of the deck. These worksheets explains how to find the length of a segment when given the values of two other segments. Your students will use these worksheets to learn how to calculate line lengths inside and outside of circles by using tangents.