We work on calculating the volume and area of cylinders, cones, spheres, pyramids, and prisms. If you have trouble on this, scroll past the worksheets. There is a complete explanation available there for each of these shapes. When we work with cylinders the volume is defines as base times height and the area is defined as Pi times the square of the radius. The volume of a cone is Pi times the square of the radius time one-third height. Spheres are a little less complicated the area is the product of four, pi, and the square of the radius. The most difficult task for students is understanding if they are working with pyramid or a prism. Make sure to sit back and take a good look before attempting each problem. These worksheets explains how to find the volume or surface area of 3-D shapes. Students should already have a foundation in using basic geometric calculations.
Print Prisms, Pyramids, Cylinders, Cones, and Spheres Worksheets
Click the buttons to print each worksheet and associated answer key.
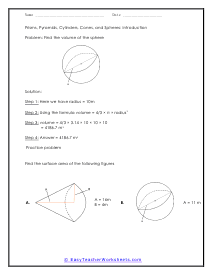
Prisms, Pyramids, Cylinders, Cones, and Spheres Lesson
This worksheet explains how to find the volume of a sphere. A sample problem is solved, and two practice questions are provided.
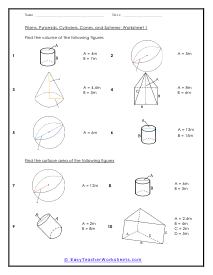
Prisms, Pyramids, Cylinders, Cones, and Spheres Worksheet
Students will find the volume or surface of the figures as indicated. Ten questions are provided.
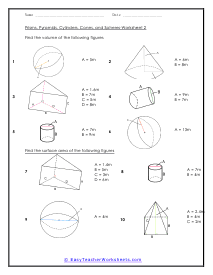
Practice Sheet
Students will find the volume or surface of the 3-D shapes provided. Ten questions are provided.
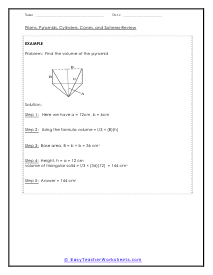
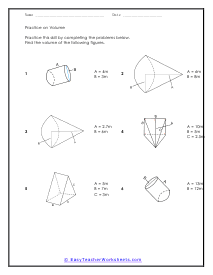
Practice Sheet 2
Students will practice finding the volumes of 3-D shapes. Six practice questions are provided.
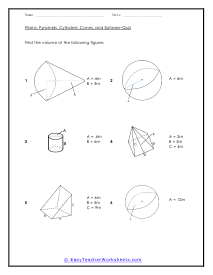
Pyramids, Cylinders, Cones, and Spheres Quiz Page 1
Students will demonstrate their proficiency in finding the volume or surface of the 3-D shapes. The first 6 of 10 problems are provided.
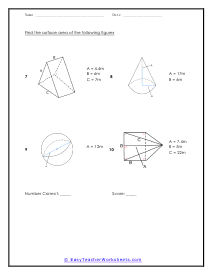
Prisms, Pyramids, Cylinders, Cones, and Spheres Quiz Page 2
Students will demonstrate their proficiency in finding the volume or surface of the 3-D shapes. The problems 7 - 10 of 10 are provided.
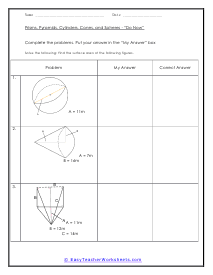
Worksheet Check
Students will find the volume or surface area of the 3-D shapes. Space is included for students to copy the correct answer when given.
How to calculate the volume and area of Prisms, Pyramids, Cylinders, Cones, and Spheres:
We utilize different approaches to define the characteristics of a geometric shape. However, one way to define the geometric shape is through volume and area.
In math, the area is known as the space that is occupied by the surface of an object or a shape. Volume is defined as the three-dimensional space occupied by an object. Three-dimensional objects/ shapes are those solid figures that possess three dimensions, i.e., height, length, and width.
Cones - Cones are 3D figures with two faces and one edge. They are pointy at one end and flat on the other end. That means they have a point on one end and a circle on the other end.
Volume - To find the volume of a cone, we use the following formula.
V= 1/3 π x r2 x h. Where, π (constant) = 3.14 | r is the radius of a circle and h is the height of the cone.
Area -To find the area3 of a cone, we use the following formula: Surface area = πrs + πr2.
Where, π (constant) = 3.14 | r is the radius of a circle and s is slanting side.
Spheres - Spheres are defined as a perfectly symmetrical 3D shape with zero vertices and one surface. Each point on the surface of the sphere is at the same distance from its center.
Volume - To find the volume of the sphere, we use the following formula: V= 4/3 x π x r3
Where, π (constant) is 3.14 | r is the radius of the sphere.
Area - To find the area of the sphere, we use the following formula: Surface Area = 4 πr2
Where, π (constant) is 3.14 | r is the radius of the sphere.
Cylinder - Cylinders have two round shapes at both ends and two parallel lines joining the round ends. To find the formula of a cylinder, we use the formula
Volume - To find the volume of the cylinder, we use the following formula: V= π x r2 x h
Where, π (constant) is taken as 3.14. r is the radius of the circular end of the cylinder and h is the height of the cylinder.
Area - To find the area of the cylinder, we use the following formula: Surface Area = 2 πrh + 2 π r2
Where, π (constant) is taken as 3.14. r is the radius of the circular end of the cylinder and h is the height of the cylinder.
Prisms - A prism has three sides with three edges and two triangular bases. Its sides are in rectangular, and the edges of triangular prism connect the corresponding sides. It bases have equilateral triangles with their edges being parallel to each other.
Volume - The volume of the prism is found by the formula, V= 1/2 x b x h x l
Where, b is the base length. h is the height of the triangle. l is the length between the triangular bases.
Area - The area of the prism is found by the formula, Surface Area = 2b + Ph
Where, b is the base length. h is the height of the triangle. P is the perimeter of the prism.
Pyramids - The pyramid is defined as the polyhedron shape that has a base and three or more triangular faces meeting at an apex.
Volume - The volume of the pyramid is found by the formula,
Volume = 1/3 l x w x h Where, l is the base length, w is he base width, and h is the height of pyramid.
Area - The area of the pyramid is found by the formula,
Surface Area = 2(b x s) + b2
Where, b is the base and s is the slanting side.


