What Are Geometric Dilations? In geometry, it is a change that transforms the length of all line segments with the same proportion. This change only transforms the size of the figure instead of its shape. That's why experts say that dilations are not isometries. The actual shape and its figure are the same due to the invariant shape under a geometric dilation. Here, it means the mathematical correspondence that is; Congruent angles : Proportional sides - You will not see any change in the size of the figure when dilation is equal to one. So, the process will be identity dilation. The image will reduce when the proportion is less than one. Greater than one proportion increases the figure's growth. Isometries, collinearity, and angle measures are invariant under a dilation. The sequence of isometries relates two congruent triangles together as well as the two similar ones with a dilation. In simple words, with two corresponding triangles, you can make one triangle from the second one by using isometries to turn it around and a dilation to transform the size. You can also understand the geometric dilation with this definition as well; In geometry, dilation is a proportional expansion or contraction of an image.

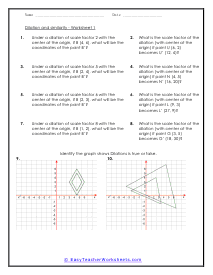
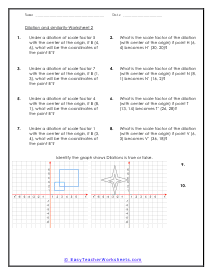
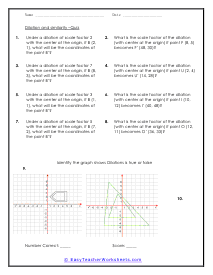
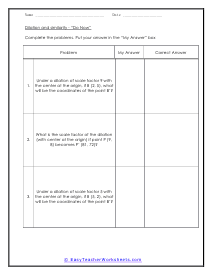
If you take a look at two similar geometric shapes you will notice that they have corresponding sides. The ratio between those sides is referred to as the scale factor. We can use this scale factor to learn the length of unknown sides of similar shapes. A dilation is a change in scale factor and can grow or shrink. In these problems you will try to determine the scale factor of dilations. You will also work on determining the position of coordinates after dilations occur. These worksheets explains how to find the scale factor of the dilation. Your students will use these activity sheets to learn how to determine the scale factors and changing coordinate points for the geometric dilations of different shapes with their centers at their origin.