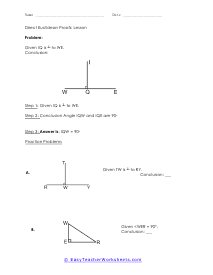
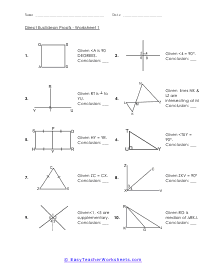
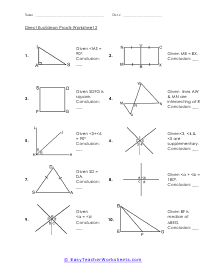
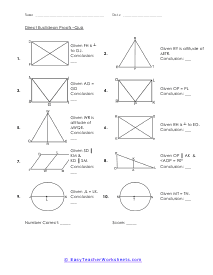
What are Direct Euclidean Proofs? At the point when you are composing a proof, you need to recollect that your contention could be that something is valid or bogus. In any evidence, you will require a constant flow of realities that can undoubtedly be built up. Your initial step is to distinguish theory and end. We need to expect that the theory is precise and valid. You will, at that point, need to perceive what you are really going after to have the option to demonstrate your decision. Direct verifications were viewed as the birth offspring of the epic Greek mathematician Euclid. From the beginning, we are going to attempt to utilize just proofs 1-4, as Euclid did, just like his normal thoughts. Those hypothesize as follows: 1) We can draw a limited line section between any two distinct focuses. 2) We can expand a limited line section to the extent that we need in a line. 3) We can draw a circle on the off chance that we are given a middle and a point on the perimeter. 4) All correct edges (half of a "straight edge") are equivalent.

When you are writing a proof you have to remember that your argument could be that something is true or false. In any proof you will need a steady stream of facts that can easily be established. Your first step is to identify a hypothesis and conclusion. We have to assume that the hypothesis is accurate and true. You will then need to see what you are working with to be able to prove your conclusion. Direct proofs were seen as the birth child of the epic Greek mathematician Euclid. These worksheets explains how to do Euclidean Proofs. Your students will use these activity sheets to learn how to apply standard Euclidean proofs to identify the types of shapes, angles, and other components being demonstrated (right angles, isosceles triangles, etc.).