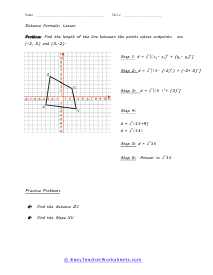
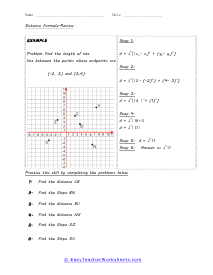
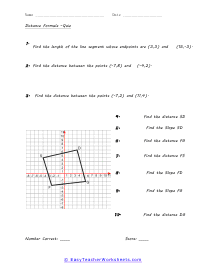
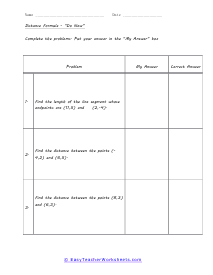
What is the Distance Formula? Definition: The Distance Formula is the best way to find the length of the gap between two points. It is the derivative of the Pythagorean Theorem. That is: a2 + b2 = c2 | cc = hypotenuse | aa & bb a right triangle | We use this formula to calculate the right angle's hypotenuse (cc) length. Distance Formula as a part of Pythagorean Theorem - The distance (d) among two points: A = ( x1 , y1 ) and B = ( x2 , y2 ). Set above the values by using the following distance formula: d = √( x2 - x1 )2 + ( y2 - y1 )2. Example: Find the length of the gap between the two points ( -3, 2 ) and ( 3,5 ). Put all the values in the formula correctly. X1 = -3 and y1 = 2 and X2 = 3 and y2 = 5 d = √( x2 - x1 )2 + ( y2 - y1 )2 d = √ ( 3 - (-3)2 + ( 5 - 2 )2 d = √(6)2 + (3)2 d = √36 + 9 d = √45 d = √9 × √5 d = 3 √5
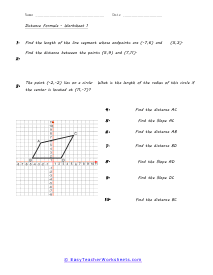
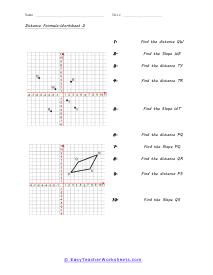
If you have two points and want to know the distance between those points, we can use this formula. It is actually a clever application of Pythagorean Theorem. The formula is the square root of the sum of the squared difference in x-axis values and the squared difference in y-axis values. The distance is equal to the hypotenuse of the right triangle formed between the two points. When it comes to trajectory calculation, this skill is paramount for many engineers and mathematicians. These worksheets explains how to find the distance (length) or slope of a segment. Your students will use these activity sheets to learn how to calculate the lengths of different lines as plotted on coordinate graphs, or within circles.