What Are Geometric Ellipses? In coordinate geometry, there are a lot of plane curves that you will come across. Some of these include parabola, hyperbola, and ellipse. Many people get confused between ellipses, circles, and ovals, while all three of these shapes are completely different. To understand an ellipse, we can say that this plane curve looks like a squashed circle. It is a plane curve surrounding two focal points. For all points on the curve, the sum of the two distances to the focal points is a constant. This plane curve has several similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. Its definition is, "An ellipse is the set of all points on a plane whose distance from two fixed points F and G add up to a constant."
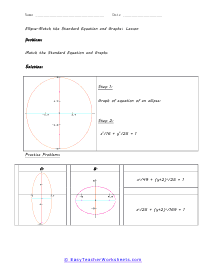
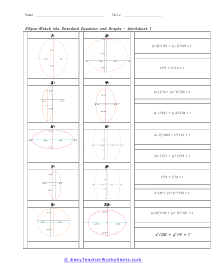
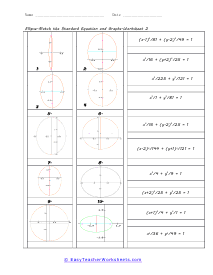
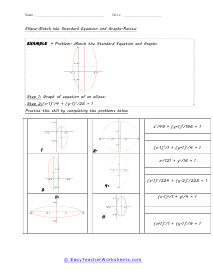
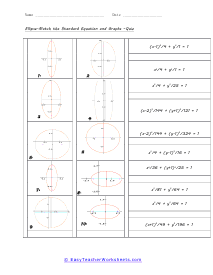
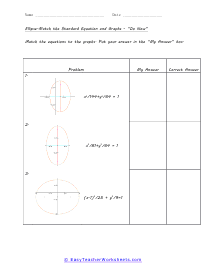
An ellipse has been said to resemble and egg or a squashed circle. Distinct points on the ellipse are called foci. The vertices are the point where the major and minor axis intersect. With this collection of worksheets we ask students to first match a graph to an equation. We then move on forward with the anatomy of ellipse including determining foci, vertices, and co-vertices. These worksheets explain ellipses, their graphs, and writing their standard equations. Activities include finding the foci, vertices, and co-vertices of a given ellipse, matching standard expressions with the correct graphs, and more.