What Are the Functions: Cos, Sin, and Tan? Cos - Cos function, or as some people call it cosine function in every triangle, is that ratio which is spotted on the opposite side of the hypotenuse of that same triangle. The cos function is considered as one of the three primary parts of trigonometry and is also a component of the sine (i.e., co + sine) Sin - The sin in the right-angle triangle can be found by dividing the length of the opposite side by size of the hypotenuse. The sine function, alongside with tangent and so sine, is among the three most usual and ordinary trigonometric functions. In the right-angled triangle, the sine of the desired angle is the length of the hypotenuse separates the distance of the opposite side. The sine is written without the 'e' as 'sin' in the formula. Tan - The tan is basically sin(x)cos(x) and hence the tan function is not identified whenever cos(x)=0. Likewise, the sin function and tangent function become zero as soon as the integer of both of them becomes a multiple of π.

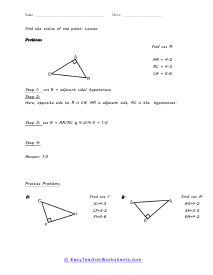
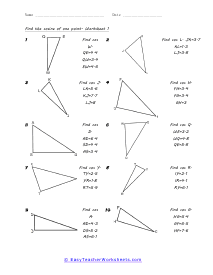
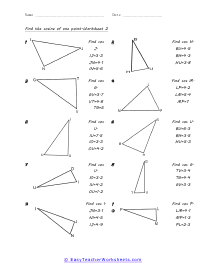
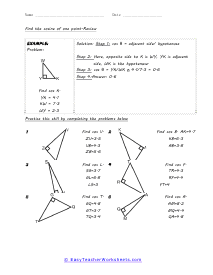
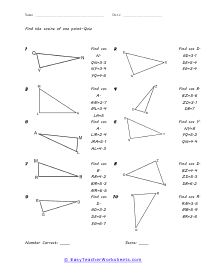
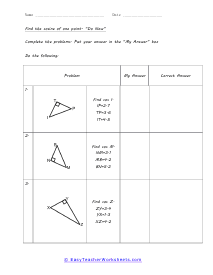
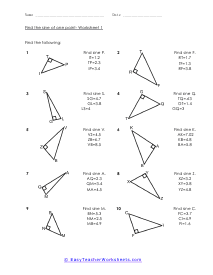
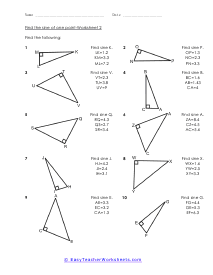
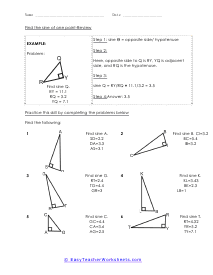
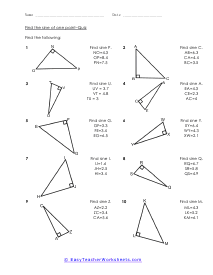
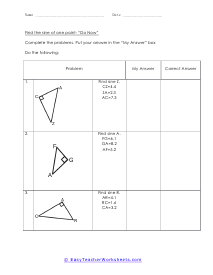
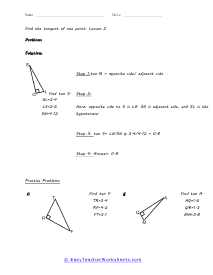
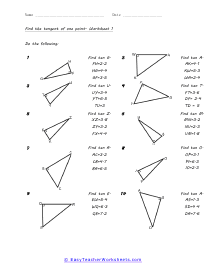
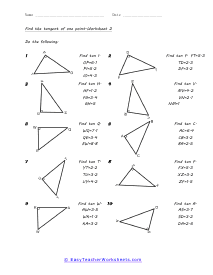
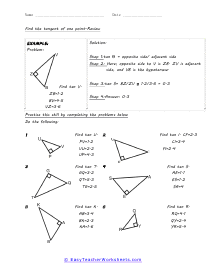
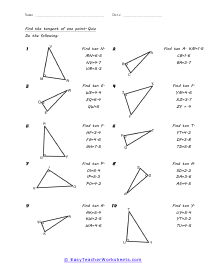
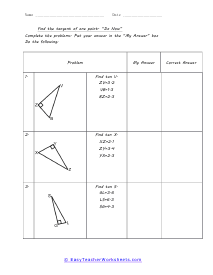
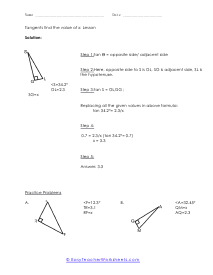
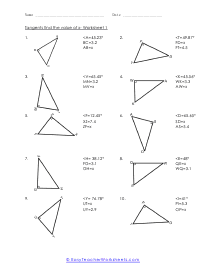
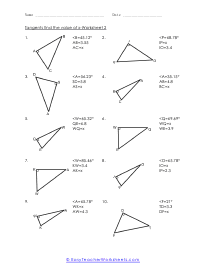
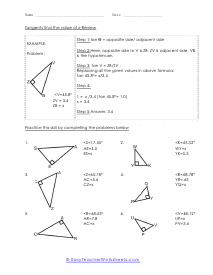
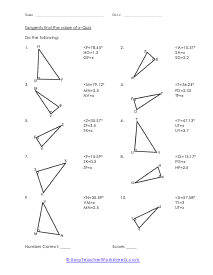
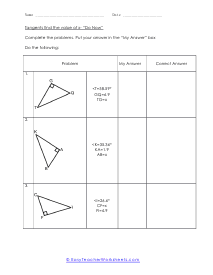
When we work with triangles a helpful acronym to learn is SOH-CAH-TOA. These relate the various sides of a triangle: Adjacent, Hypotenuse, and Opposite sides. The Adjacent side is next to the angle theta. The Hypotenuse is the longest side. The Opposite side is the side that is directly opposite angle theta. Using the main functions of trigonometry Sine, Cosine, and Tangent; we can determine missing sides with the help of that acronym. (SOH) Sine theta is equal to the Opposite side divided by the Hypotenuse. (CAH) Cosine theta is equal to the Adjacent side divided by the Hypotenuse. (TOA) Tangent theta is equal to the Opposite side divided by the Adjacent side. This set works with triangles of various sizes and amplitudes. Your students will use these activity sheets to practice calculating the sine, cosine, and tangent for various triangles, as well as using those values to determine leg length. This is a heavy engineering unit.