What Is the Difference Between Lines and Planes? A line is distinct as a line of the point that spreads extremely in two orders. A plane is called by three points that are not on a similar line. Here below, we see the plane ABC. Space extends infinitely in all directions and is a set of all points in three dimensions A line in two the plane has the form: ax + by = c. There are only two degrees of liberty here; the proportion matters. This is equivalent to the plane in three-space, which has a similar linear equation: ax + by + c z = d. Again, only the proportion a: b:c: d matters, here are three degrees of liberty. The equation for a line in three planes is more complex. A line is the juncture of two planes so that we can specify both planes, with two equations: ax + by + c z = d and ex + f y + g z = h. Usually, a parametric vector equation is easier to deal. We specify a point on the line (a, b, c) and a direction vector (d, e, f) and we have real parameter ranging over the reals, so the line is simply (x, y, z) = (a, b, c) + t (d, e, f) which easily generalizes to more dimensions.

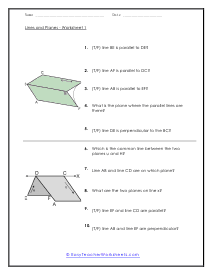
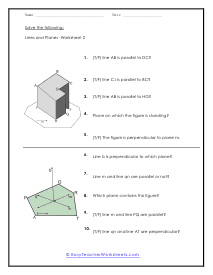
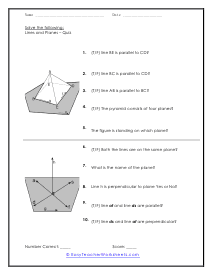
As we explored in another section of worksheets, lines are points that extended infinitely in the exact opposite direction. Planes are similar in that they have a set of points extending infinitely. Planes have these points arranged so that they form a flat connected surface. Planes therefore have infinite length, width, and height. Planes are usually drawn as four-sided objects. With this collection of worksheets you will use your understanding of line geometry to make inferences between figures. These worksheets explain how to determine the relationship between lines in a 3-dimensional figure. Most of the questions are True/False, but some require specific answers.