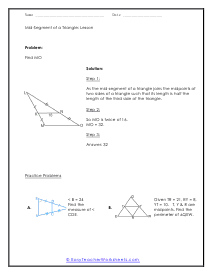
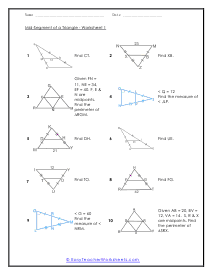
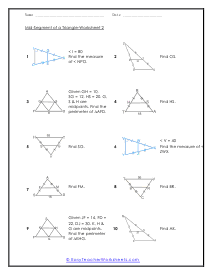
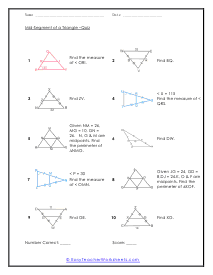
What are Mid-Segments of Triangles? Triangles are simple two-dimensional shapes that have three sides, three vertices, and three angles. There are right triangles, where the angle opposite to the hypotenuse is 90°, then there are isosceles triangles with two equal sides and two equal angles, scalene is a triangle that has no equal sides and no equal angles, the equilateral triangles have three equal sides and three equal angles. When solving triangles, you will come across a term, "mid-segments." Mid-segment is a term that is defined by "a segment that connects the midpoints of two sides of a triangle." Midsegments follow these properties; These are always parallel to the third side of the triangle. These are always equal to half the length of the third side. There are three possible midsegments in triangles, depending on which pair of sides is initially joined.

After we learn to calculate the midpoints of a line segment, we transfer that skill to triangles. A midsegment of a triangle is a line segment that connects the midpoint of two sides of the triangle. This segment will always be parallel to the third side which is not connected. This cabinet of worksheets will have you first draw a midsegment of a triangle and then determine the value of angles within the triangle. These worksheets explain how to find the measure of sides and angles of a triangle using midsegments. Students will also use the information about the mid-segments to calculate angles, find perimeters, and more.