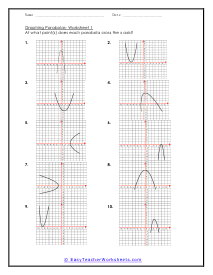
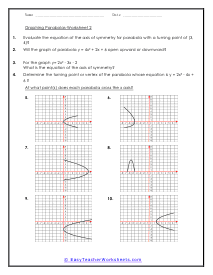
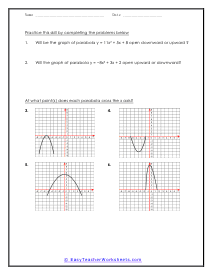
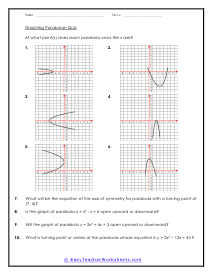
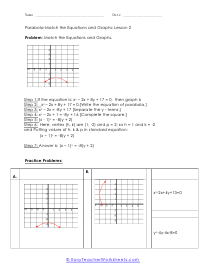
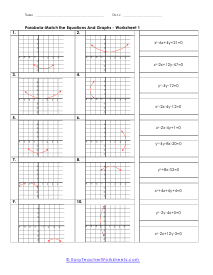
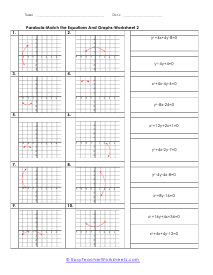
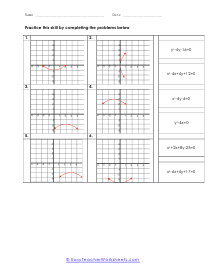
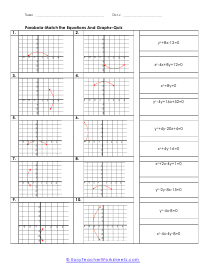
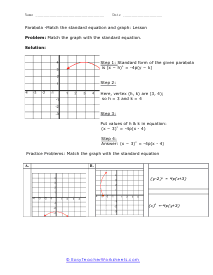
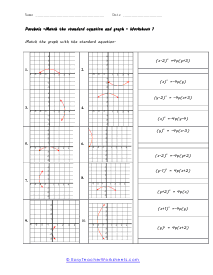
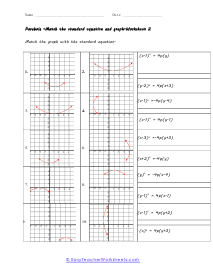
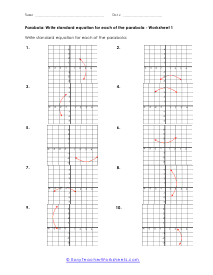
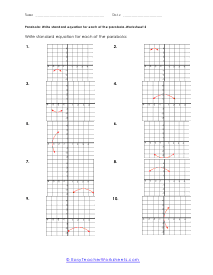
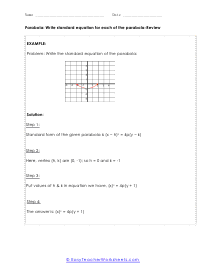
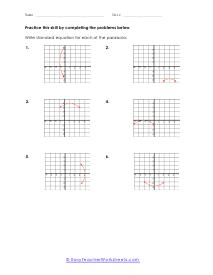
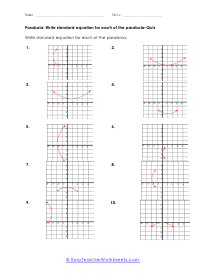
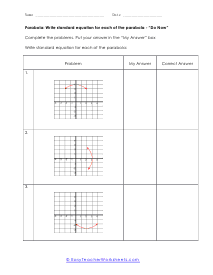
What are Parabolas? In mathematics, a parabola is defined as the symmetrical open curve, which is formed by the intersection of a cone with a parallel plane to its side. To put it simply, a parabola is a curve where any given point lies at an equal distance from a fixed straight line and a fixed point. A parabola comes with several features that define its placement and shape on the cartesian plane. Vertex - Vertex is defined as the extreme point of the parabola. If the parabola opens down, the vertex will be the highest point on the graph. If the parabola opens down, then the vertex will be the lowest point on the graph. In both cases, the vertex is represented as the turning point of the parabola. Axis of Symmetry - The axis of symmetry lies parallel to the y-axis, and it's the line drawn vertically through the vertex. x-intercept - The point on the cartesian plane where the parabola crosses the x-axis is known as the x-intercept. The number of x-intercepts depends on the location of the graph on the plane. y-intercept - The point on the cartesian plane where the parabola crosses the y-axis is known as the y-intercept.

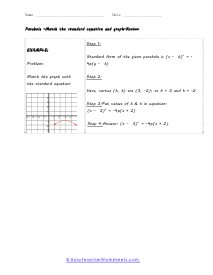
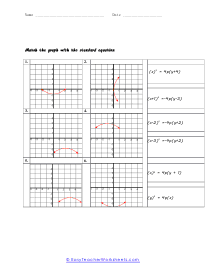
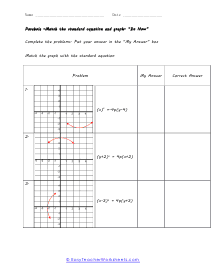
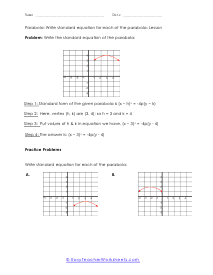
When you finally start to study physics a great deal of time is spent learning about trajectory. Trajectory is the path an object travels (on Earth) due to gravity. These trajectories often follow the shape of a parabola. What goes up must come down. A parabola is a curve where any point is an equal distance from a fixed point (focus) and a straight line (directrix). The exact point where the parabola hits a sharp turn is called the vertex. In this section you will interpret graphs of parabolas as well as identify the anatomy of parabolas. These worksheets explain how to graph parabolas and write the standard equations for parabolas. They will also calculate focus, vertex, and directrix, match parabolic equations with the correct graphs, write equations, and more.