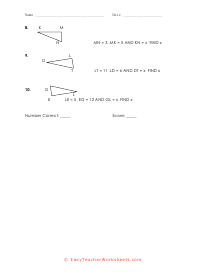
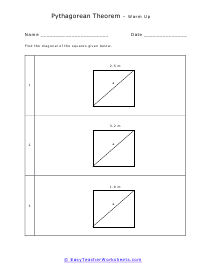
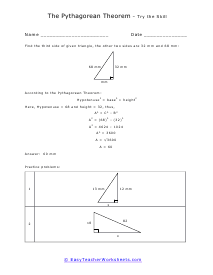
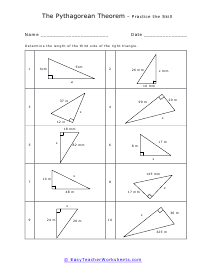
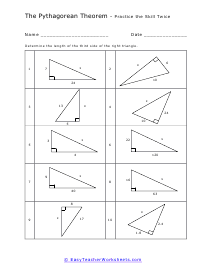
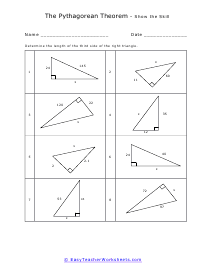
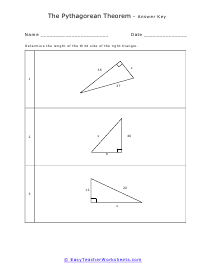
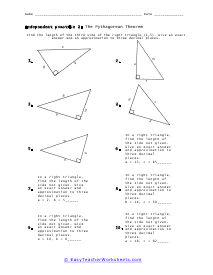
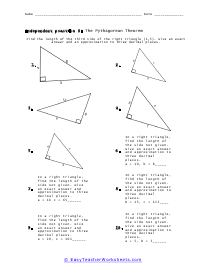
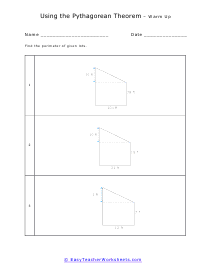
What is the Pythagorean Theorem? Pythagorean theorem describes the relation between the sides of a right-angled triangle. The Pythagorean formula is applied on a right-angled triangle and is used to determine the hypotenuse, base and the perpendicular of the triangle. The theorem states that: "In a right-angled triangle, the square of the hypotenuse side is equal to the squares of the perpendicular side and the base side." The hypotenuse is the longest side, and perpendicular is the side opposite to the hypotenuse side. Consider the triangle above, where a is the perpendicular side, b is the base side, and c is the hypotenuse. According to the definition of the Pythagorean theorem, the formula would be written as: c² = a² + b²

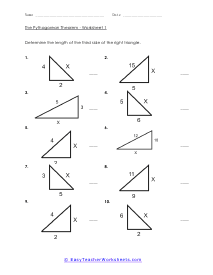
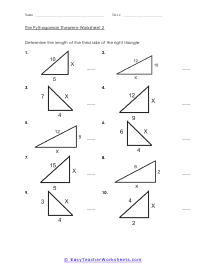
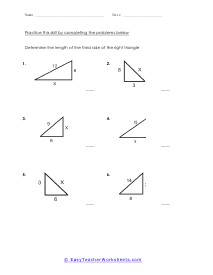
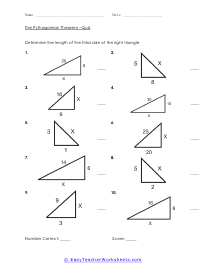
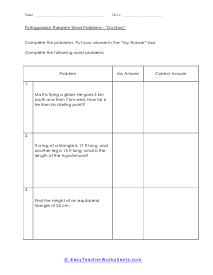
When a triangle has a right-angle, we can use the sum of the squares of each leg of the triangle to find the squared value of the hypotenuse. It can be rearranged to find the length of any of the sides. The Pythagorean Theorem has so many different applications to everyday life that it is not even funny. The theorem allows us to completely understand a right-triangle system with ease. It is used measure distances that are applicable to everything from measuring a deck about to be constructed or building a skyscraper. Your students will use the theorem to solve for variables for given triangles. Some questions may be in the form of word problems. Students should be familiar with different types of triangles.