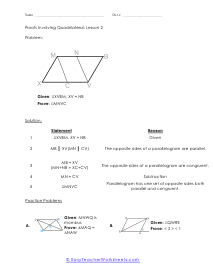
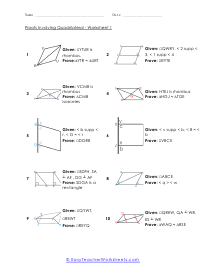
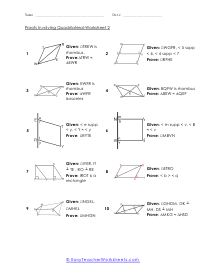
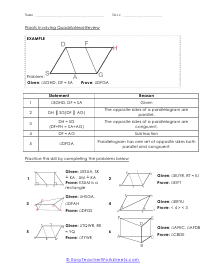
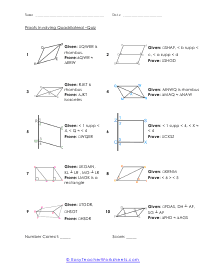
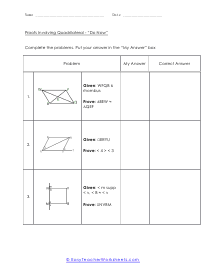
Tips for Writing Proofs Involving Quadrilaterals - With regard to math, you must have the option to demonstrate that what you're doing is right. With regard to geometry, it's the equivalent. In geometry, you'll regularly be approached to demonstrate that specific shape is, without a doubt, that specific shape. For instance, you may be indicated a quadrilateral and be approached to demonstrate that it is a parallelogram. Recollect that a quadrilateral is a four-sided level shape. A parallelogram is a quadrilateral with two sets of inverse, equal sides. Seeing this shape, you may imagine that it is a parallelogram, yet except if the issue explicitly lets you know. Additionally, you can demonstrate that it is, you can't state without a doubt that it's a parallelogram.

In this section of lessons and worksheets we will learn how to work with proofs that involve four-side closed figures. You will need to provide the facts that are noted in the figure based on your knowledge of quadrilaterals You will primarily base all of your work on the four fundamental facts of quadrilaterals. A parallelogram has two pairs of parallel sides. Rectangles have four right angles. A rhombus has four congruent sides. A square has four congruent sides and angle. The following activity sheets ask your students to prove or disprove a given statement about a quadrilateral using proofs. While some proofs are given, students should be familiar with the larger set.