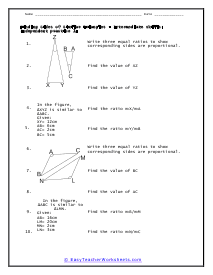
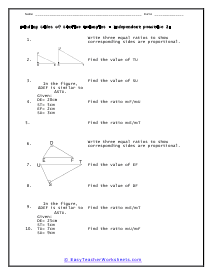
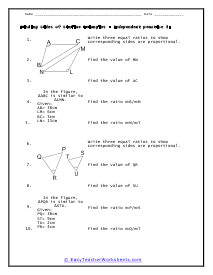
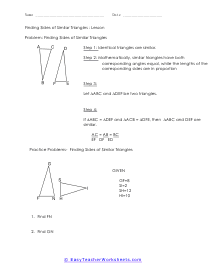
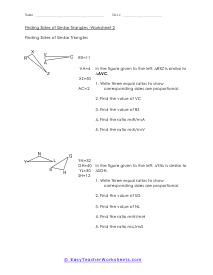
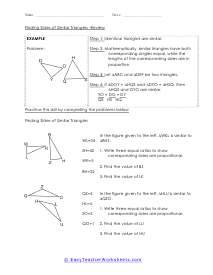
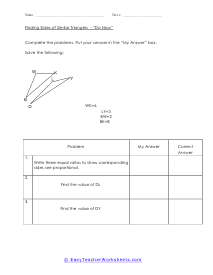
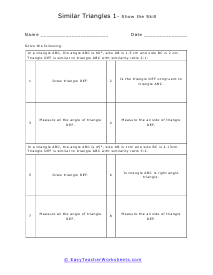
What Are Similar Triangles? These are triangles that have the same shape, and their sizes are dynamic. With these corresponding shapes the corresponding angles will be congruent, and the side will have equal proportion when the pair of the triangle is similar. The symbol of such triangles is ~. Similar triangles formula: we can explore the sides of one triangle by another triangle. We can use the following expressions to find the valid angles and length of the sides of any two triangles; ∠A = ∠X, ∠B = ∠Y, ∠C = ∠Z, AB/XY = BC/YZ = AC/XZ Condition for the similar triangle: If you have the smallest polygon that has three sides, the condition for similar triangles is: Equal corresponding angles , Proportional corresponding sides Examples: Problem#1: We have △ ABC & △APQ, and the length of their sides are; AP= 5cm, PB= 10cm, BC= 20cm And, PQ that is parallel to BC Here, you have to find PQ. Solution: In both triangles, the angle is the same, and ∠APQ = ∠ABC are corresponding angles. △ ABC ~ △ APQ - AP/AB= PQ/BC -> (1) Putting the values in eq(1), 5/15 = PQ/20 - PQ= 20/3 cm

When we are sure that we have two triangles that are similar, you can learn the measures of all the angles and sides with a simple application. Similar triangles are the same in every way expect for size. We often mark corresponding sides and angles to tell us that those measures are equal. The goal should be to find the ratio between the corresponding sides or angles. Once you find the value of that scale, you just need to apply that proportion to calculate all of the measures. These worksheets explain how to use similar triangles to find the measure of the length of other triangles.