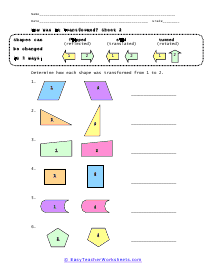
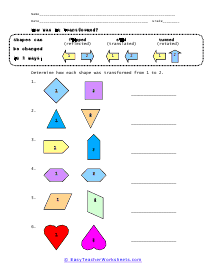
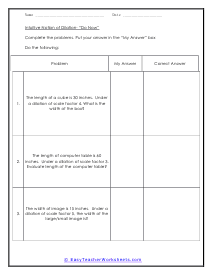
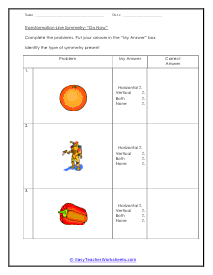
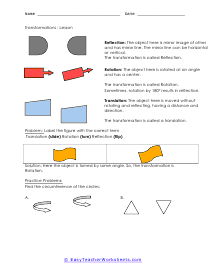
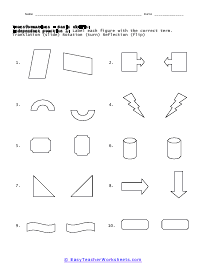
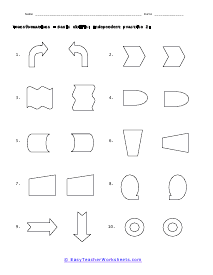
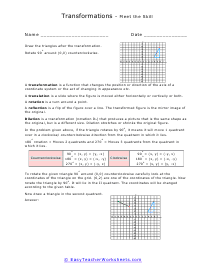
Geometric transformation involves converting a preimage into an image. We convert or mold the preimage by changing its dimension and shape. Typically, transformation is divided into two types: - The rigid transformation doesn't change the size or shape of the preimage. - The non-rigid transformation that alters the size of the preimage while maintaining the shape. Rigid and non-rigid transformations are further divided into different categories. Rotation, translation, and reflection are the types of rigid transformation, and dilation is the type of in the non-rigid transformation. Below we have briefly discussed each type of transformation. Dilation - Dilation is the transformation that expands or contracts the shape without changing its orientation or shape. Translation - Translation slides or moves across the plane or through space. In translation, all points of a figure move or slide in the same direction and cover the same distance. Rotation - Rotation moves the figure about a line or point. It basically means to spin or turn the figure at a point. The point of turning or spinning is known as the center of rotation. This center can lie outside the figure or be present on the figure. Reflection - Reflection involves flipping the shape across the line to create a mirror image, in the mirror image, the measures of lines and angles are preserved.
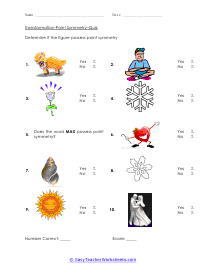
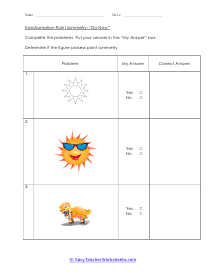
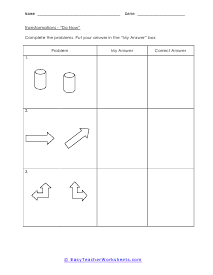
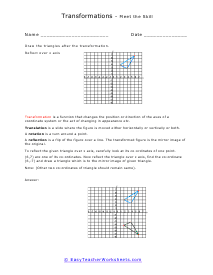
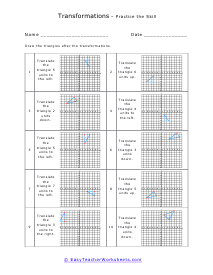
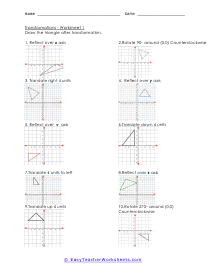
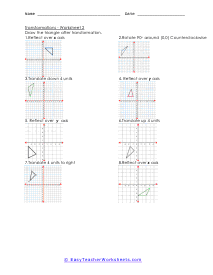
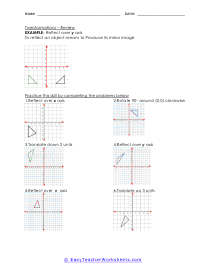
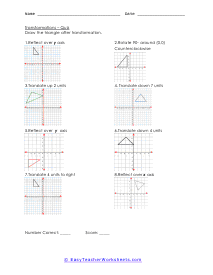
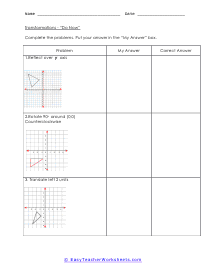
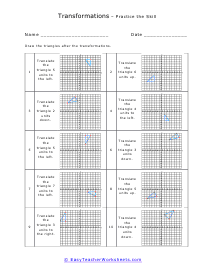
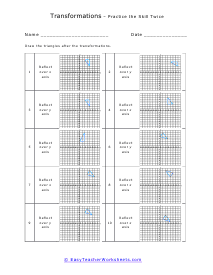
A transformation is when a figure changes position in some way. There are four common transformations of figures including dilation, rotation, reflection, and translation. Dilation is when a figure reduces or enlarges in size. Rotation is when a figure moves around its own center. Reflection is when the figure flips over a line. Translation is when a figure slides in any direction. Over the course of these worksheets and lessons you will examine each of the four common transformations. These worksheets explains how to recognize and draw transformations. These worksheets contain easy and intermediate activities to teach students about shape transformation, including dilation, line and point symmetry, reflection, rotation, and translation. Some exercises contain coordinate graphs to assist with plotting.