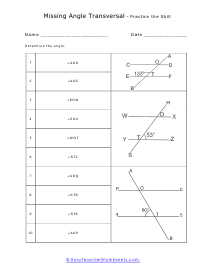
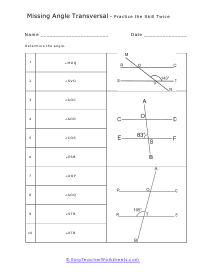
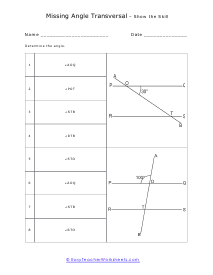
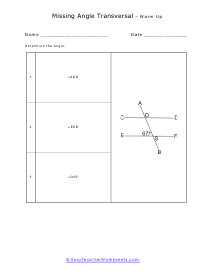
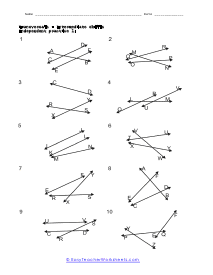
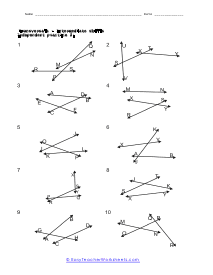
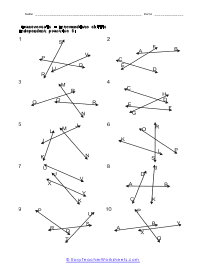
What Are Transversal Lines? A transversal is when two parallel lines are intersected by the third line at an angle. The line intersecting the two parallel lines; the third line is known as the transversal line. We get different types of angles when a transversal line passes through the parallel lines. Some of the commonly known angles are defined below: Supplementary angles - When pair angles are added together and give us a measure of 180 degrees, we get supplementary angles. When we put the pair of supplementary angles together, we can draw a straight line across the two angles. Or simply put, the two angles, when put together, will make a half-circle. Also, the supplementary angles aren't limited to transversals. Interior Angles - As the name implies, angles present interiorly, on the inside, of the two parallel lines are known as the interior angles. Exterior Angles - Angles present on the outside of the two parallel lines are known as the exterior angles. Corresponding Angles - Angles that are present on the same side of the transversal line are known as the corresponding angles. In corresponding angles, one angle is an interior angle while the other is the exterior angle; these angles are equal in measurement and are congruent. Whenever you go on to study math, do you think that the subject is boring? Well, everyone thinks that there is not a single thing about math that makes sense and could b fun or interesting to study about. But that's not true! Math has its fair share of exciting topics that is actually very interesting and very fun to learn about!

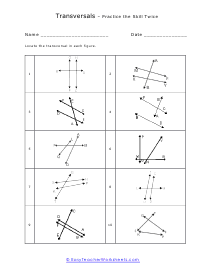
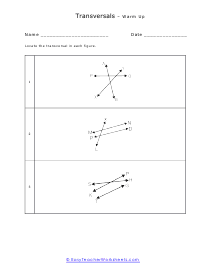
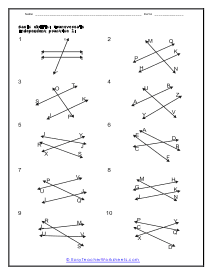
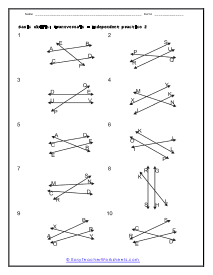
When you come across a line that breaks across two other lines it is called a transversal line. When a transversal cuts across parallel lines we quick determine the value of all the angles by just knowing the measure of one of the angles. Vertical opposite angles (the angle opposite the known angle) are equal. Supplementary angles will then add to one-hundred and eighty degrees. That gives us all the measures of the angles around the known angle. We can then identify an alternate exterior or interior angle pair. There measures will be equal. We can then repeat this procedure to determine all angles around that line and the cutting line. These worksheets explains how to find and determine the angle of a transversal. Instructors please note that some examples may not contain any transversals.