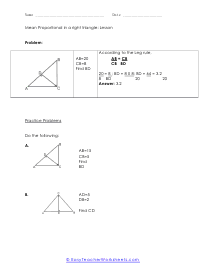
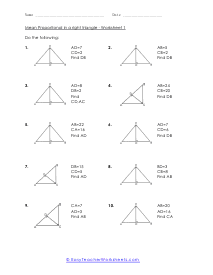
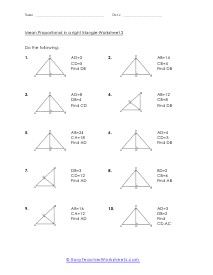
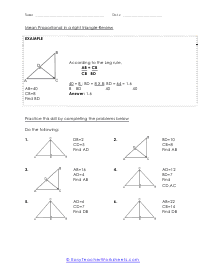
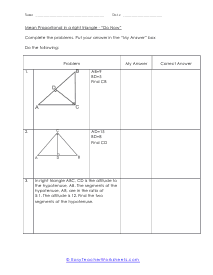
What is Meant by a Mean Proportional in a Right Triangle? Mean proportional (or geometric methods) show up in two famous hypotheses concerning right triangles. Before we express these hypotheses, we should investigate a hypothesis identifying with the triangles we will utilize: Theorem: The height to the hypotenuse of correct triangle structures, two triangles that are like one another, and to the first triangle. The leg of a correct triangle is the mean corresponding between the hypotenuse and the projection of the leg on the hypotenuse. The projection of a leg is that portion of the hypotenuse, which is appended to contiguous the leg. A projection is framed by dropping an opposite from the finish of the portion leg to the hypotenuse.

When we take a right triangle and sit it down on the hypotenuse side (longest side is the base we can start to learn a great deal more about the measures in that triangle. If we draw a line of altitude to the right angle from the hypotenuse, we will form two triangles. Not only that, those are similar triangles and they are similar to our original triangle. The reason they are similar is that all of the triangles are composed of the same angles. This allows us to use the mean proportional to determine the lengths the hypotenuse has been divided into. It says the that the length of the left section of the hypotenuse divided by the altitude is proportional to the altitude divided by the length of the right section of the hypotenuse. These worksheets explains how to find the mean proportional in a right triangle. Your students will use these activity sheets to learn how to calculate the mean proportional of right triangles using the "leg rule."