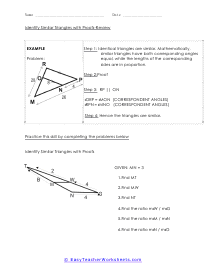
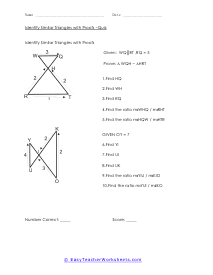
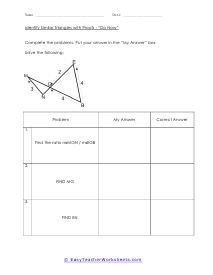
How Do Prove the Similarity of Triangles? Similar figures are defined as geometric figures that have the same shape but different sizes. Typically, we use three theorems to establish the similarity of the triangles. The three theorems involved are, side-angle -side (SAS), Angle- Angle (AA), and Side-Side-Side (SSS). Angle-Angle (AA) Theorem - Angle-Angle (AA) theorem says that two triangles are similar if the two pairs of their corresponding angles are congruent. They might appear as identical. To establish them as congruent using this theorem, you only have to compare the two pairs of corresponding angles. Side-Angle-Side (SAS) Theorem - This theorem follows the order of a side, an included angle, and then a side. The SAS theorem says that two triangles are similar if two sides of a triangle are proportional to the two corresponding sides of second triangles, and the included angles are congruent. Side-Side-Side (SSS) Theorem - The last theorem telling us about the congruency of a triangle, states that if all three sides of one triangle are proportional to all three corresponding sides of the second triangle, then those two triangles are congruent.

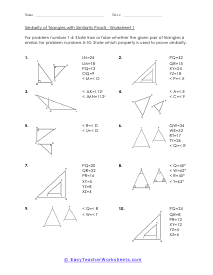
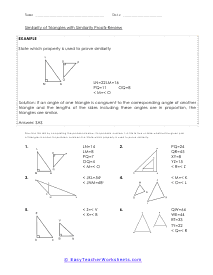
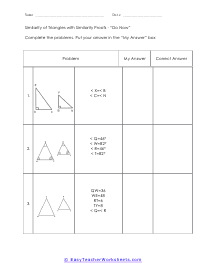
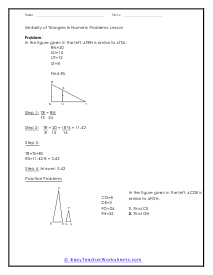
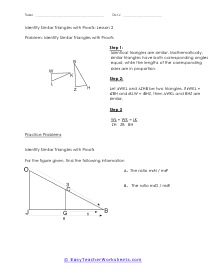
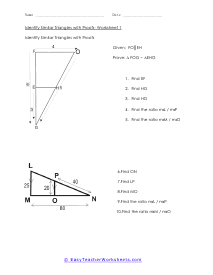
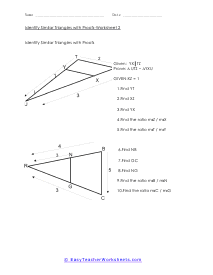
In triangle geometry we are often trying to prove that two or more triangles are similar. If they are similar they are not the same exact, but their corresponding angles and sides are in proportion to each other. We can prove similarity using a number of different methods and it is all situational based. We can use the Angle-Angle Similarity Postulate if both triangles have a two pairs of congruent angles. If the lengths of corresponding sides of the triangles are proportional, we can use the Angle-Angle Similarity Postulate. If they share a congruent angle and the corresponding legs of that angle are equal in length, we can use the Side-Angle-Side Similarity Theorem. These worksheets explains how to determine if triangles and similar and how to use similarity to solve problems. Your students will use these activity sheets to identify similar triangles by applying the correct proofs, as well as calculate segment lengths. Students should already be familiar with the applicable proofs and formulas.