In math we use Venn diagrams to help us understand and display relationships between collections of things. Venn diagrams can get very complex and contain multiple circles, but here we are just going to use the standard form of Venn diagrams. This allows us to compare two distinct characteristics of the data and where our collections of things fall into those categories.

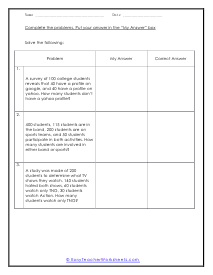
How Do You Use Venn Diagrams in Logic Problems? Venn diagrams are also called primary diagrams, set diagrams, or logic diagrams. John Venn was the first to introduce Venn diagrams in 1880, and since then, these diagrams have taken their name after him. Venn diagram organizes information without making it look dull and boring. It solves complex mathematical questions. It helps reason logic and compares the data set. Venn diagrams are drawn in circles, overlapped on each other, to simplify logical problems and questions. The organized information and graphical representations differentiate between two sets or more items. These worksheets explain how to create and manipulate the use of Venn diagrams. Your students will use the following activity sheets to learn how to construct Venn diagrams to sort data sets and answer questions about them. Note that extra paper will be required.