What are common number rules? In mathematics, there are multiple rules, but some of them we use while solving sets. They have individual names and symbols. Natural Numbers (N) - These are number set in which we include all numbers starts from zero till the end of counting. We denote this rule of common name by N. For example, {1, 2, 3, ......} or { 0, 1, 2, 3, ......}. Integers (Z) - These are the number set in which we include whole numbers and negative whole numbers both. It depends on the type of question that either we use only negative integers in one set, only positive integer in each set, or both together. We express this number of rule by Z. For Example, A = { 1, 2, 3, ......} , B = { -1, -2, -3, ......} , and { -1, -2, -3, 0, 1, 2, 3}. Rational Numbers (Q) - These are the number sets in which we include all value in fractional form. We can also add integers in it as fractional value. We denote it by Q that means it is quotient as we use R for the set of real numbers. We can make another set related to rational number that is irrational number. We don’t include rational numbers in it. For Example: 3/2 = 1.5 , -1/1000 = 0.001, 8/4 = 2. There are other number rules that are common in math practices including algebraic numbers, transcendental numbers, real numbers, imaginary numbers, complex numbers.

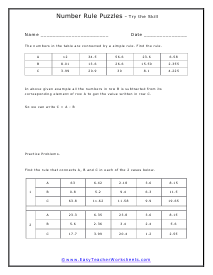
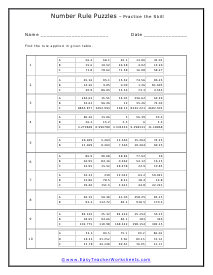
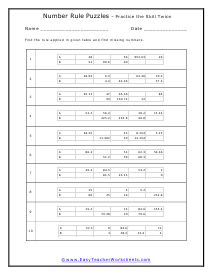
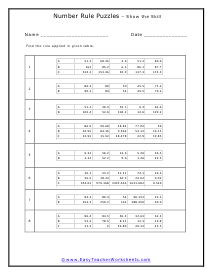
This is a really fun section for students because they are applied math problems. I sometimes refer to these as Code Breakers because you are trying to decipher the code of the patterns that you are presented with and then filling in the missing pieces. This will require you to take your math skills to the next level. We suggest you focus on the gaps between each set of the sequence and then compare them to learn the pattern that you see. These worksheets explain how to identify the equation that forms the rule for a given table. Students will also fill in any missing numbers in the table.