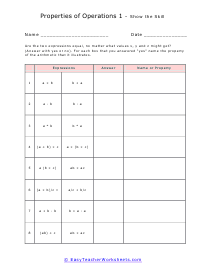
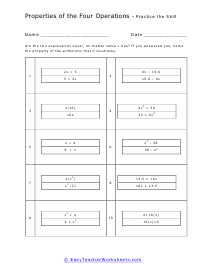
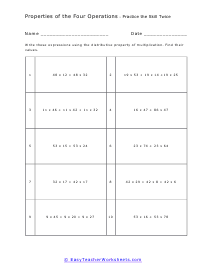
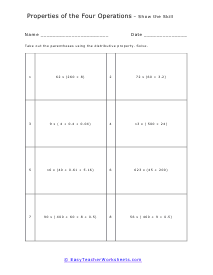
There are four basic arithmetic operations, and these include addition, subtraction, multiplication, and division. The properties of operations include commutative, associative, distributive, identity, closure. Closure: When the answers fall into the original set, we call this the closure. If you add two even numbers, the answer is still an even number, the set of even numbers is closed under addition (has to closure). When two odd numbers are added, the answer is not an odd number, the set of odd numbers is not closed under addition (no closure). Commutative: The property of numbers when the order of the sum does not make a difference, i.e., a+b=b+a. This does not work for subtraction and division but only for multiplication and addition. Associative: The change of position of parenthesis does not affect the answer. This does not work for subtraction and division but only for multiplication and addition. Identity: Adding zero (identity) to a number gives the same number as the answer. Any number added to its additive inverse equals zero. For multiplication, the identity is 1. This does not work for the division as dividing a number by zero results in infinity, but only for multiplication, addition, and subtraction. Distributive Property: The property using which we pass the number value outside of the parentheses, using multiplication, to the numbers being added or subtracted inside the parentheses. To apply the distributive property, it must be multiplication outside the parentheses and either addition or subtraction inside the parentheses.

This is a wonderful section for students to review all the properties of operations. In other sections of our site we breakdown each operational property separately, but in this section we mash them altogether. We do spend some time describing the differences that lie between the associative and commutative properties. We also brush of the identity property that basically says anything that is added to zero is itself. Your students will practice applying the associative, commutative, and distributive properties in order to solve various equations. Though all equations have been provided, students should have seen this material before.