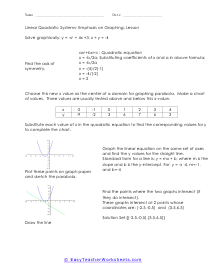
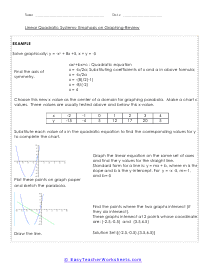
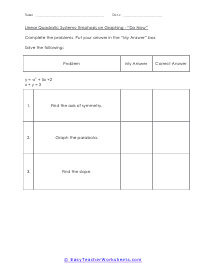
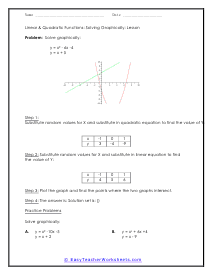
Equations of linear functions are graphed as straight lines because the x variable does not have an exponent. Quadratic functions are graphed as curves because the variable does have an exponent. Linear and quadratic equations can be solved either algebraically or graphically. In these worksheets, student will learn how to solve linear and quadratic functions graphically. They will first find the axis of symmetry. They will then use the value of the variable as the center of a domain for graphing each parabola. They will graph the linear equation on the same set of axes and find the y values for the straight line. They will then determine where the two graphs intersect. Graph paper will be required to accompany these worksheets. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, reviews, and quizzes. When finished with this set of worksheets, students will be able to solve linear and quadratic functions graphically.
Quadratic equations are the ones where the highest power of the variables is 2. The general form of a quadratic equation is given by; ax2+ bx + c = o. There are four methods to solve quadratic equations. Factoring, completing the square, quadratic formula, and graphing. Using graphs is one of the easiest ways to solve quadratic equations. Before we get started, you must know that the roots of a quadratic equation are the x-intercepts of the graph. Use a table to draw the graph of the equation. The points on the x-axis that the graph passes through are the roots of the equation. These worksheets explain how to solve linear and quadratic equations graphically. Sample problems are solved and practice problems are provided.