The probability that is defined as the possibility for the likelihood of the following event based on the result of the previous event. Conditional probability is found out by multiplying the probability of the previous into the expectation of the succeeding event. For example: You have event A that represents that there is a 20% chance of rain today. You have event B that represents that you have to go outside and has a probability of 60%. The conditional probability will give you the outcome based on the relationship between these two events. That is the chance value that represents both, you need to go outside, and it is raining. Independent events are events that are not affected by one another. For example, tossing a coin. In a coin toss, each toss is an independent event and an isolated outcome. Events can also be dependent. That is, both the events are affected by each other. The next event is affected by the possibility of the previous event. For example, 2 blue and 3 red balls are in the bag. The probability of getting a blue ball is 2 in 5. But if we got a red ball before, then the likelihood of getting a blue is 2 in 4. Conditional probability is the likelihood of event A occurring, given that event B has occurred.

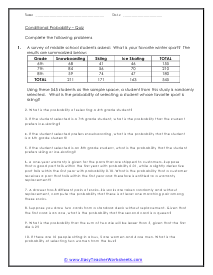
In these worksheets, the conditional probability problems are presented as word problems. Students will read the word problems and determine the prospective outcome that is being requested. Students may require blank paper to use to do their work. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, a review, and a quiz. Worksheets are also provided that students can use for independent practice. When finished with this set of worksheets, students will be able to determine the known probability of a statement. These worksheets explain how to determine conditional probability. These word problems directly relate to every day work students will need to cover and handle with great ease.