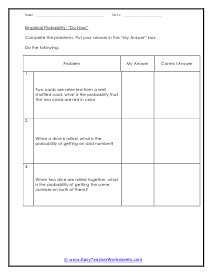
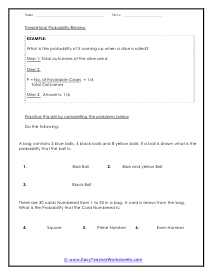
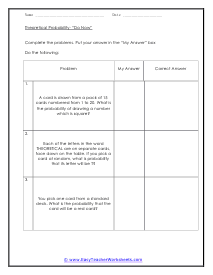
Home > Math Worksheets > Statistics > Empirical and Theoretical Probability

The empirical probability (also known as relative frequency or experimental) of an event is expressed as a ratio of the number of outcomes in which a specified event occurs to the total number of trials in an actual experiment. Theoretical probability is based on thinking through the situation. It is expressed as a ratio of the number of favorable outcomes to the number of possible outcomes. In these worksheets, students will learn about the differences and exceptions between the theoretical and empirical forms. They will learn to identify when a calculated likelihood is theoretical and when it is empirical. They will solve problems to calculate both empirical and theoretical forms of possibility. This set of worksheets contains lessons, step-by-step solutions to sample problems, both simple and more complex problems, reviews, and quizzes. When finished with this set of worksheets, students will be able to calculate and differentiate between empirical and theoretical forms of possibilities.

Typically, probability is the likelihood of the occurrence of an event. We can write it in the forms of decimals and fractions. When probability is represented in decimal form, it ranges for 0 to 1. When an event shows a likelihood of 0, it means that a particular event has zero chances of taking place. However, when an event has a likelihood of 1, it means that a particular event will take place. When the likelihood is closer to 1, then the event is likely to happen, and when the likelihood is closer to 0, then it is less likely that an event would happen. For instance, an event with a likelihood of 0.7 is more likely to happen than an event with a likelihood of 0.1 Empirical probability is the type of prospect that is calculated by doing experiments and conducting observations. The likelihood that the event will happen is based on the results obtained from the collected data. The mathematical formula for calculating empirical probability is written as: Empirical = Number of times an event can take place / total number of trials. For instance, a fair die is rolled 180 times, and you to find out the number of times 4 turned up. We know that each number on the die has an equal probability of 1/6. Therefore, the probability of 4 turning up is also 1/6. So, we will calculate 180 x 1/6= 30. The expectation of 4 is 30 out of 180. These worksheets explain how to determine and differentiate between empirical and theoretical probability. Sample problems are solved and practice problems are provided.

Get Free Worksheets In Your Inbox!

Empirical and Theoretical Probability Worksheets

Click the buttons to print each worksheet and answer key.

Empirical Probability Lesson

This worksheet explains how to determine empirical probability when rolling dice. A sample problem is solved, and two practice problems are provided.

Empirical Probability Worksheet

We tackle word problems that focus on these concept and work on making solid decisions with them. Example problem: Each of letters in the word ASSUMING are on separate cards, face down on the table. If you pick a card at random, what is the probability that its letter will be U or S?

Practice

We apply this approach to some unique story based real world problems. For example: A company is producing bulbs and these bulbs are packed in a box but when they delivered the bulbs to its customers some of the bulbs get defective. If the probability of getting the defective bulb is 0.65 So What is the probability of getting the right bulb?

Review and Practice

Once again we are focused on empirical probability. You will be tasked with problems like: Four dice are rolled together. The sum of the number on them is 23. Find the probability that exactly one dice shows the number 5?

Quiz

Students will demonstrate their proficiency with these types of word problems. Ten problems are provided.

Check

This provides you with a nice way to introduce or review all of the concepts that we discuss with this topic.

Theoretical Probability Lesson

This worksheet explains how to determine the theoretical probability of flip a two sided coin. A sample problem is solved, and two practice problems are provided.

Theoretical Probability Worksheet

We take an approach at theoretical probability through using cards, dice, and groups of people.

Practice

We tackle problems like: A bag contains 12 yellow marbles, 14 black marbles, and 10 green marbles and you pick one without looking. What is the probability that the marble will be black?

Review and Practice

The concept of how to determine theoretical probability is reviewed. A sample problem is solved. Six practice problems are provided.

Quiz

Students will demonstrate their proficiency with all of the skills and concepts that we have explored with this topic. Ten problems are provided.

Check

We use a different type of playing cards on this worksheet. A card is drawn from a pack of 15 cards numbered from 1 to 20. What is the probability of drawing a number which is square?

Theoretical vs. Empirical Probability Lesson

This worksheet explains how to differentiate between theoretical and empirical probability. A sample problem is solved, and two practice problems are provided.

Theoretical vs. Empirical Probability Worksheet

You will need to make a judgement call as to how you approach each problem. Example exercise: Amana can hit a target 3 times in 6 shots, Jasmine can hit the target 2 times in 6 shots and Claudia can hit the target 4 times in 4 shots. What is the probability that at least 2 shots hit the target?

Practice

We approach these problems in a much different manner. Example: A programmer noted the results of attempting to run 20 programs. The results showed that two programs ran correctly in the first attempt, 7 ran correctly in the second attempt, 5 ran correctly in the third attempt, 4 ran in the fourth attempt, 2 ran in the fifth attempt. What is the probability that his program will run correctly on the third run?