What is the Probability of Mutually Exclusive Events? When you're dwelling in the deep world of statistics, there is a concept which encapsulates the entire field of natural mathematics. That concept is the occurrence of mutually exclusive events. Mutually Exclusive Event are those events which cannot occur at the same time. Let's take the example of a coin toss, in which you can either get heads or tails. Now the probability of any mutually exclusive event depends on the number of occurrences possible. In other words, if you have a dice, you have a maximum of six possibilities out of which one will occur. However, considering a coin toss, there is a 50-50 chance of any occurrence.

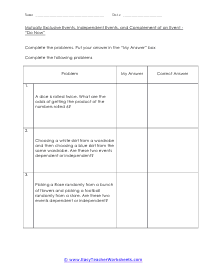
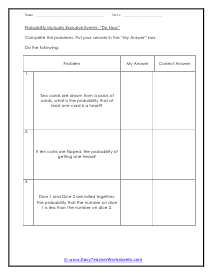
In these worksheets, students will dive deeper into the study of probability. A basic understanding of the concept of probability and how to calculate probability is required. In these worksheets, students will learn what the terms mutually exclusive, independent, and complement mean and how they apply to probability. Students will determine if the probability of an event is mutually exclusive, independent, or complement. Students will learn how to calculate the probability of mutually exclusive events. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, a review, and a quiz. It also includes ample worksheets for students to practice independently. When finished with this set of worksheets, students will know how to determine if events are mutually exclusive, independent, or complements and how to calculate the probability of mutually exclusive events. These worksheets explain how to determine if events are mutually exclusive, independent, or complements and how to calculate the probability of mutually exclusive events. Sample problems are solved and practice problems are provided.