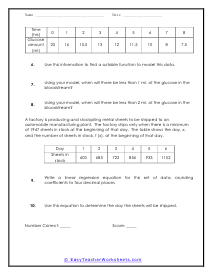
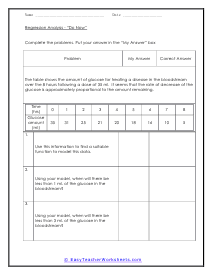
In these worksheets, students will write linear regression equations and use the equations to solve problems.

Home > Math Worksheets > Statistics > Regression Analysis

Regression is the process by which the relationship between two variables is determined. In linear regression analysis, the dependent variable is thought to be related to the independent variable or variables in a linear way. Regression analysis is the branch of mathematical analysis. This method is the combination of several practical processes for recognizing the level of dependence among variables using statistical data. The information is not enough about the distributions of the variables under consideration. With this fact, you can characterize the regression problem in mathematical statistics. For example, random variable Y.Y. has probability distribution at fixed value XX of the other variable such as; E(Y | x) = g(x, ß), E(Y | x) = g(x, ß), set of unknown parameters is ß Determining function is g(x) The result of observation lets you determine the value of these parameters. You can use the process of regression in various apps of statistics. It has two core types that are; Predictions - we use regression analysis to generate predictions. Correlation - It is a model that we gain by regression analysis. It is suitable for some kind of data better than others. With it, you can refine a statistical model to add additional inputs.

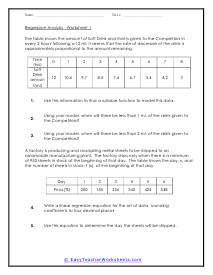
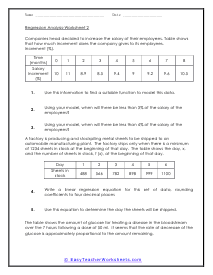
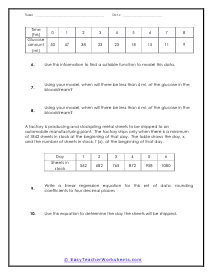
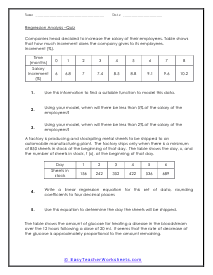
In these worksheets, problems are presented as word problems. Student will learn how to write a linear regression equation and use the equation to solve a problem. Worksheets provide tables of progressing information for students to refer to in solving problems. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, a review, and a quiz. It also includes ample worksheets for students to practice independently. When finished with this set of worksheets, students will be able to write linear regression equations and use the equations to solve problems. These worksheets explain how to write linear regression equations and use the equations to solve problems. Sample problems are solved and practice problems are provided.



Get Free Worksheets In Your Inbox!

Regression Analysis Worksheets

Click the buttons to print each worksheet and answer key.

Regression Analysis Lesson

We yake students through this sample problem: : A factory is producing and stockpiling metal sheets to be shipped to an automobile manufacturing plant. The factory ships only when there is a minimum of 1135 sheets in stock at the beginning of that day. The table shows the day, x, and the number of sheets in stock, f (x), at the beginning of that day. Write a linear regression equation and use this equation to determine the day the sheets will be shipped.

Print Now!

Lesson and Practice

Students will use this information to find a suitable function to model this data.

Print

Worksheet Page 1

Students will write a linear regression equation and use the equation to solve problems like: The table shows the amount of Soft Drink and that is given to the Competitors in every 2 hours following a 12 ml. It seems that the rate of decrease of the drink is approximately proportional to the amount remaining. Use this information to find a suitable function to model this data. Using your model, when will there be less than 1 ml. of the drink given to the competitors?

Print

Worksheet Page 2

This goes hand and hand with the previous sheet. You will use jumping in a pool data and auto manufacturing data models to answer a series of problems. The last five of ten problems are provided.

Print

Regression Analysis Practice Page 1

Students will practice writing linear regression equations to model company bonuses and car manufacturing. The first five of ten problems are provided.

Print

Practice Page 2

A factory is producing and stockpiling metal sheets to be shipped to an automobile manufacturing plant. The factory ships only when there is a minimum of 1842 sheets in stock at the beginning of that day. The table shows the day, x, and the number of sheets in stock, f (x), at the beginning of that day. Write a linear regression equation for this set of data, rounding coefficients to four decimal places.

Print

Review Page 1

You will model the data for manufacturing metal sheets. To calculate the days the sheets will be shipped: Substitute the value of x in the linear regression equation and calculate the value of y. The value of x for which y becomes equivalent to 1200.

Print

Review Page 2

You model data that includes running a length of distance, metal plant production, and glucose use in humans. Six practice problems are provided.

Print

Quiz Page 1

Students will demonstrate their proficiency in writing linear regression equations and explaining the data that they are assigned to model. The first five of ten problems are provided.

Print

Quiz Page 2

Students will demonstrate their ability with this skill from a different angle. The second of ten problems are provided.

Print

Regression Analysis Skills Check

The table shows the amount of glucose for treating a disease in the bloodstream over the 8 hours following a dose of 35 ml. It seems that the rate of decrease of the glucose is approximately proportional to the amount remaining. Using your model, when will there be less than 1 ml. of the glucose in the bloodstream?

Print