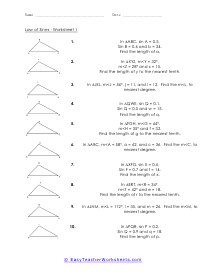
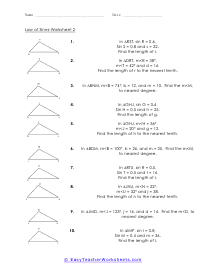
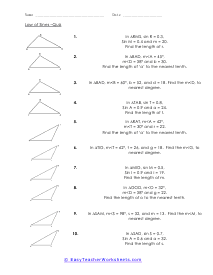
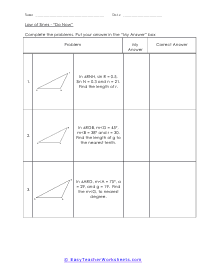
The Law of Sines is an equation that describes the relationship between the lengths of the sides of any shape (in this case triangles) to the sines of its angles. When the Law of Sines is used to determine the missing measurement values of a triangle when given two sides and an angle opposite one of those sides (SSA), it is called the Ambiguous Case. This law is the connector between the oblique angles and the sides of a triangle. To put it differently, it simply is the ratio of one of the side’s length and the sine of the opposite angle. In retrospect, for a triangle ABC which is oblique with the sides a, b, and c, the law of sines will be: a / sin⁡A = b / sin⁡B = c / sin⁡C. To use the Law of Sines, you need to know either two angles and one side of the triangle (AAS or ASA) or two sides and an angle opposite one of them (SSA).

There are 12 worksheets in this set, divided into two sets of 6. In the first set, students will use the Law of Sines to solve problems. In the second set, students will use the Law of Sines and the Ambiguous Case. These are moderately complex problems and a sound understanding of trigonometry is required in order for students to be successful with these worksheets. This set of worksheets contains step-by-step solutions to sample problems, both simple and more complex problems, a review, and a quiz. It also includes ample worksheets for students to practice independently. Most worksheets contain between eight and ten problems. When finished with this set of worksheets, students will be able to use the Law of Sines and the Ambiguous Case. These worksheets explain how to use the Law of Sines and the Ambiguous Case. Sample problems are solved and practice problems are provided.