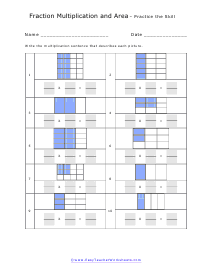
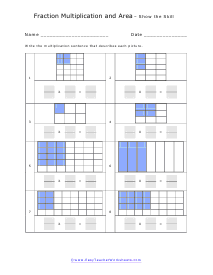
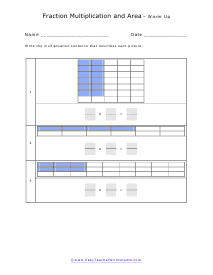
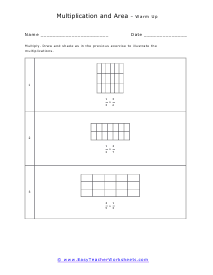
You will be confronted with visual fractions based on rectangles. Make sure to go deeply through the lesson that accompanies each section so that you fully understand what is expected of you. You will need to count how many sections are found across the shape (that is your first denominator), count how many of them are shaded (that is your first numerator). Then repeat the same procedure vertically and you will have both fractions. To determine the area of a rectangle just find the product of the length and breadth (width).

How do you write a multiplication sentence based on a fraction? Recall that duplication is an alternate route for rehashed expansion. It is an approach to include a similar number of gatherings, a few or "different" times. To discover the result of a part and an entire number, convert the entire number to a division before duplicating. Recollect that an entire number can be composed into a part as the number over a denominator of 1. In the first place, change the entire number to a division. 4 = 41 Revamp the issue with the part. 19 × 41 At that point, increase the two parts. Increase the numerator by the numerator and the denominator by the denominator. 1 × 49 × 1 = 49 The subsequent part is in the least difficult structure. The item is 49. The commutative property of increase expresses that the request where you duplicate numbers don't make a difference as the item will be the equivalent. These worksheets explain how to describe the area of a shape by using a multiplication sentence. Your students will use these worksheets to multiply fractions as represented by shaded sections of shapes in order to determine what part of the total area is shaded.